X 4 X 2 X
sicesbrasil
Sep 22, 2025 · 7 min read
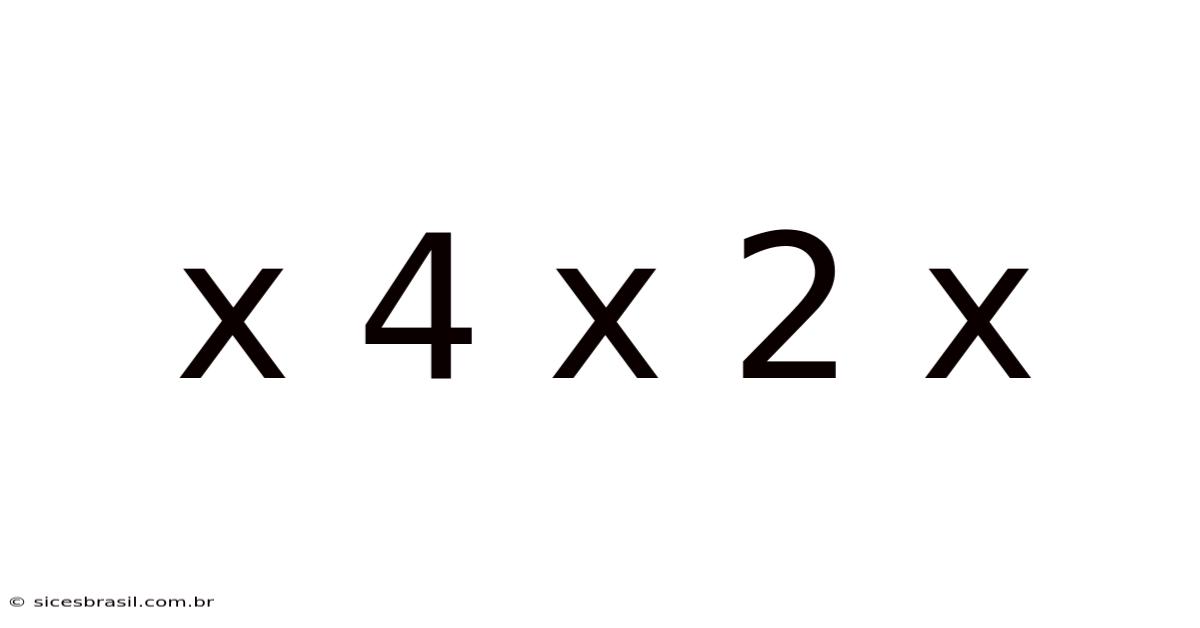
Table of Contents
Decoding the Mystery: A Deep Dive into X x 4 x 2 x and its Implications
The seemingly simple expression "X x 4 x 2 x" might initially appear straightforward, but it opens a fascinating door into the world of mathematics, specifically algebra, and its applications in various fields. This article will delve into the meaning, interpretations, and implications of this expression, exploring its potential uses and expanding on its underlying principles. We'll move beyond the basic arithmetic to uncover its power as a building block for more complex mathematical concepts.
Introduction: Understanding the Basics
At its most fundamental level, "X x 4 x 2 x" represents a mathematical expression involving multiplication. The 'X' is a variable, a placeholder for an unknown value. The numbers 4 and 2 are constants, their values are fixed. The presence of an 'x' at the end is ambiguous; we will explore this ambiguity and how to address it.
The core concept lies in the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Since we only have multiplication here, the order doesn't strictly matter; we can multiply the numbers in any sequence. However, the presence of the final 'x' necessitates careful interpretation.
Interpreting the Ambiguous 'x'
The most crucial aspect of understanding "X x 4 x 2 x" is clarifying the meaning of the trailing 'x'. There are several possibilities:
-
Typographical Error: The most likely scenario is that the final 'x' is a simple typographical error. If this is the case, the expression simplifies to: X x 4 x 2 = 8X. This is a linear expression, a fundamental building block in algebra.
-
Implied Variable: It's possible that the final 'x' represents a second variable, distinct from the initial 'X'. In this case, the expression becomes: X x 4 x 2 x Y (where we've replaced the second 'x' with 'Y' for clarity). This results in the expression 8XY, a term representing the product of two variables. This is frequently encountered in areas like geometry (calculating areas), physics (representing forces), and various other fields.
-
Implied Multiplication by an Unknown Factor: This interpretation suggests that the final 'x' signifies an unknown multiplicative factor, representing something yet to be defined or determined within a larger problem. This is common in problem-solving and modelling scenarios where certain parts of the equation are still undefined.
-
Part of a Larger Expression: The entire expression "X x 4 x 2 x" may be a fragment of a more complex equation. The final 'x' might serve as a placeholder within a larger mathematical structure, for example, within a series of terms being added or subtracted. Consider this possibility: (X x 4 x 2 x) + 5 = 21. Here, solving requires understanding the context of the full expression.
Mathematical Implications and Applications
Regardless of the interpretation of the final 'x', the core expression highlights crucial mathematical concepts:
-
Variables and Constants: The distinction between 'X' (a variable) and 4 and 2 (constants) is fundamental to algebra. Variables represent changing values, while constants remain fixed. Understanding this distinction is crucial for solving equations and modeling real-world scenarios.
-
Multiplication and its Properties: The expression demonstrates the commutative and associative properties of multiplication. The commutative property states that the order of multiplication doesn't affect the result (a x b = b x a). The associative property states that the grouping of numbers in multiplication doesn't affect the result (a x (b x c) = (a x b) x c).
-
Linear Equations: If we interpret the expression as 8X, we're dealing with a simple linear equation. Linear equations are the foundation for modeling many real-world phenomena, from calculating distances and speeds to analyzing financial trends and predicting population growth. Solving for 'X' involves isolating it using algebraic manipulation.
-
Polynomial Expressions: If we interpret the expression as 8XY, we are dealing with a basic polynomial expression. Polynomials are foundational in higher-level mathematics and are essential for representing complex relationships between variables. They have extensive use in calculus, statistics, and various engineering fields.
-
Problem Solving and Modeling: The ability to represent real-world problems using mathematical expressions like "X x 4 x 2 x" is a cornerstone of mathematical modeling. By assigning meaningful values to variables and constants, we can translate word problems into solvable equations. For example, if 'X' represents the number of apples per basket, and we have 4 baskets, each containing 2 varieties of apples, then 8X could tell us the total number of apple varieties.
Solving for X (in the simplest interpretation)
Assuming the simplest interpretation where the final 'x' is a typo, we have the equation: 8X = some value. To solve for X, we need additional information. Let's say we're given that the entire expression equals 40. Then we have:
8X = 40
Dividing both sides by 8:
X = 40/8 = 5
Therefore, in this specific scenario, X = 5. This demonstrates how a simple algebraic equation can be solved to find the value of an unknown variable.
Exploring the Quadratic Aspect (Advanced Interpretation)
Let's consider a more complex interpretation. Suppose the expression is part of a quadratic equation. A quadratic equation involves a variable raised to the power of 2 (x²). Imagine a scenario:
X² + 8X = 0
This quadratic equation can be factored:
X(X + 8) = 0
This equation has two solutions: X = 0 and X = -8.
Here, our original "X x 4 x 2 x" (interpreted as 8X) forms a part of a larger, more complex quadratic expression, showcasing how seemingly simple expressions can be components of more sophisticated mathematical structures.
Real-World Applications across Disciplines
The ability to manipulate and understand expressions like "X x 4 x 2 x," even in its simplest form, finds application across numerous fields:
-
Physics: Calculating velocity, acceleration, and force often involves similar multiplicative relationships between variables.
-
Engineering: Designing structures, calculating stresses and strains, and optimizing systems require working with algebraic expressions that often mirror the structure of "X x 4 x 2 x."
-
Finance: Calculating compound interest, determining investment returns, and forecasting financial trends rely heavily on mathematical modelling using variables and constants in multiplicative equations.
-
Computer Science: Algorithms and programming often involve iterative processes where calculations are repeated multiple times, requiring the manipulation of variables similar to those in the given expression.
-
Economics: Predicting supply and demand, analyzing market trends, and modelling economic growth require the use of algebraic equations and functions.
Frequently Asked Questions (FAQ)
-
Q: What if the expression is X x 4 x 2 x Y x Z? A: This would simply be a more complex multiplicative expression, resulting in 8XYZ. It would represent the product of four variables.
-
Q: Can this expression be used in calculus? A: Absolutely! Derivatives and integrals often involve manipulating expressions with multiple variables and constants. The basic principles demonstrated by this simple expression are crucial in these more advanced mathematical concepts.
-
Q: Is there a difference between using * and x for multiplication? A: While traditionally 'x' is used, '*' is often preferred in computer programming and more advanced mathematics to avoid confusion with the variable 'x'. Both represent multiplication.
-
Q: How important is the order of operations in this specific case? A: Because only multiplication is involved, the order does not alter the outcome, provided the final 'x' is interpreted correctly. However, understanding the order of operations is crucial in more complex equations where addition, subtraction, exponents, and parentheses are present.
Conclusion: Beyond the Surface
The seemingly simple mathematical expression "X x 4 x 2 x" serves as a powerful illustration of fundamental algebraic concepts. By analyzing its different interpretations and exploring its implications, we've uncovered its versatility and relevance across various fields. Its simplicity hides a depth that extends far beyond basic arithmetic, serving as a foundational building block for more complex mathematical models and problem-solving strategies. The core message is that even seemingly trivial expressions can unlock deep mathematical understanding when explored thoroughly. This example underscores the importance of attention to detail, clear notation, and the crucial role of context in interpreting mathematical expressions. The ability to correctly interpret and manipulate expressions like this is a key skill for success in numerous academic and professional endeavors.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 4 X 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.