X 2 X 2 6
sicesbrasil
Sep 23, 2025 · 5 min read
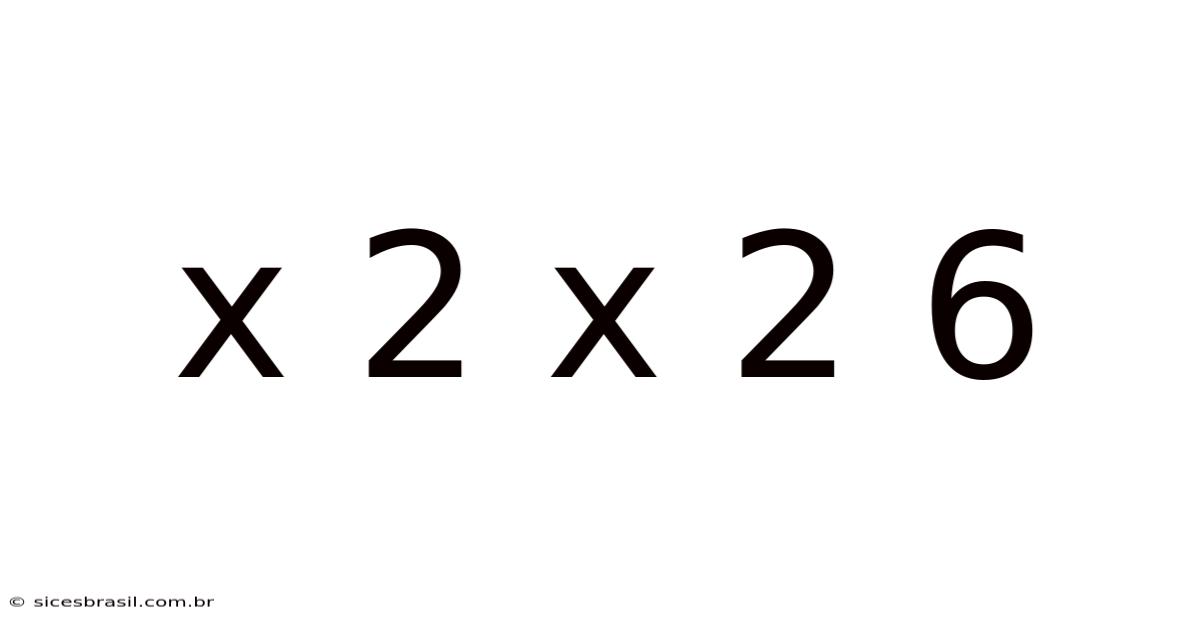
Table of Contents
Unraveling the Mystery: Exploring the Mathematical and Logical Implications of "x 2 x 2 = 6"
This article delves into the seemingly simple equation "x 2 x 2 = 6," exploring its mathematical implications, potential logical interpretations, and the broader concepts it touches upon. While at first glance it appears to be a straightforward algebraic problem, a closer examination reveals layers of complexity and opportunities for deeper learning in mathematics and logic. We'll unpack the equation, discuss its solutions (or lack thereof), and explore related mathematical ideas.
The Obvious (and Incorrect) Approach
The most immediate interpretation of "x 2 x 2 = 6" is as a simple algebraic equation. We might try to solve for 'x' using standard algebraic manipulation:
x * 2 * 2 = 6
4x = 6
x = 6/4
x = 1.5
However, this solution, while seemingly straightforward, ignores a crucial aspect: the ambiguity of the notation. The equation is inherently unclear due to the lack of parentheses or explicit indication of the order of operations.
Order of Operations (PEMDAS/BODMAS) and its Importance
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), dictates the sequence in which mathematical operations should be performed. Without parentheses to clarify the intended order, the equation "x 2 x 2 = 6" can be interpreted in multiple ways, leading to different results.
Let's examine the possibilities:
-
Interpretation 1: (x * 2) * 2 = 6: This leads to the solution x = 1.5, as calculated above. This interpretation prioritizes multiplication from left to right.
-
Interpretation 2: x * (2 * 2) = 6: This interpretation prioritizes the multiplication within the parentheses first, resulting in:
x * 4 = 6
x = 1.5
In this case, both interpretations yield the same result. However, this coincidence masks the underlying issue of ambiguity.
Exploring Beyond Standard Algebra: Logical and Set-Theoretic Interpretations
While the algebraic interpretation offers a straightforward (though ambiguous) solution, let's consider the problem from different perspectives. We can approach the problem using a more abstract, logical approach:
Question: Can we find a set or operation that, when applied twice, results in a value related to '6'?
This opens up possibilities beyond simple algebraic manipulation:
-
Set Theory: Imagine a set containing the elements {1, 2, 3}. If we define an operation ‘⊗’ such that A ⊗ B means the union of sets A and B, then:
{1} ⊗ {2} = {1, 2} {1, 2} ⊗ {3} = {1, 2, 3}
The cardinality (number of elements) of the final set is 3. This is not directly equal to 6, but it suggests a potential link between repeated operations and a resulting value.
-
Modular Arithmetic: We could interpret the equation within a modular arithmetic system. For example, in modulo 3 arithmetic, where numbers "wrap around" after reaching 3, we could potentially find a solution. However, even in this system, a direct solution to x 2 x 2 ≡ 6 (mod 3) is unlikely.
The Importance of Precise Mathematical Notation
This exercise highlights the crucial importance of precise mathematical notation. The seemingly simple equation "x 2 x 2 = 6" becomes ambiguous without clear indication of the order of operations. The use of parentheses or other clarifying symbols is essential to avoid misinterpretations and ensure that mathematical expressions are unambiguous.
Expanding the Scope: Related Mathematical Concepts
The exploration of "x 2 x 2 = 6" allows us to introduce several important mathematical concepts:
-
Order of Operations (PEMDAS/BODMAS): As previously discussed, this fundamental principle dictates the sequence of calculations.
-
Algebraic Manipulation: Solving for 'x' involves fundamental algebraic techniques, such as simplifying expressions and isolating variables.
-
Set Theory: The concept of sets and set operations provides an alternative framework for interpreting mathematical relationships.
-
Modular Arithmetic: Exploring modular arithmetic introduces the concept of different number systems and their properties.
-
Functional Equations: This problem can be viewed as a simple example of a functional equation, where we are searching for a function that satisfies a given condition.
Frequently Asked Questions (FAQ)
-
Q: Is there a single correct answer to "x 2 x 2 = 6"?
A: No, without clarifying parentheses, the equation is ambiguous. Both interpretations yield x = 1.5, but the ambiguity should be addressed.
-
Q: How can I avoid ambiguity in my mathematical expressions?
A: Always use parentheses to clearly indicate the order of operations. Be precise and consistent in your notation.
-
Q: What are some other ways to interpret "x 2 x 2 = 6"?
A: The interpretation can be extended to different mathematical systems like set theory or modular arithmetic, although straightforward solutions are unlikely in these cases.
Conclusion: Learning from Ambiguity
The seemingly simple equation "x 2 x 2 = 6" serves as a valuable lesson in the importance of precise mathematical notation and the diverse ways in which mathematical problems can be approached. While a straightforward algebraic solution exists (given certain assumptions), the lack of clarity reveals the necessity of precise language and the potential for alternative interpretations within different mathematical frameworks. The exploration of this equation offers a rich learning opportunity, touching upon fundamental algebraic concepts, set theory, and the significance of unambiguous notation in mathematics. It underscores the idea that even simple-looking problems can lead to a deeper appreciation for the subtleties and complexities of mathematics. The ambiguity itself becomes a tool for learning, prompting us to be more rigorous and precise in our mathematical thinking and communication. Remember, clear communication is crucial for any mathematical endeavor, from simple equations to advanced theorems.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 2 X 2 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.