X 2 4 X 2 2
sicesbrasil
Sep 22, 2025 · 5 min read
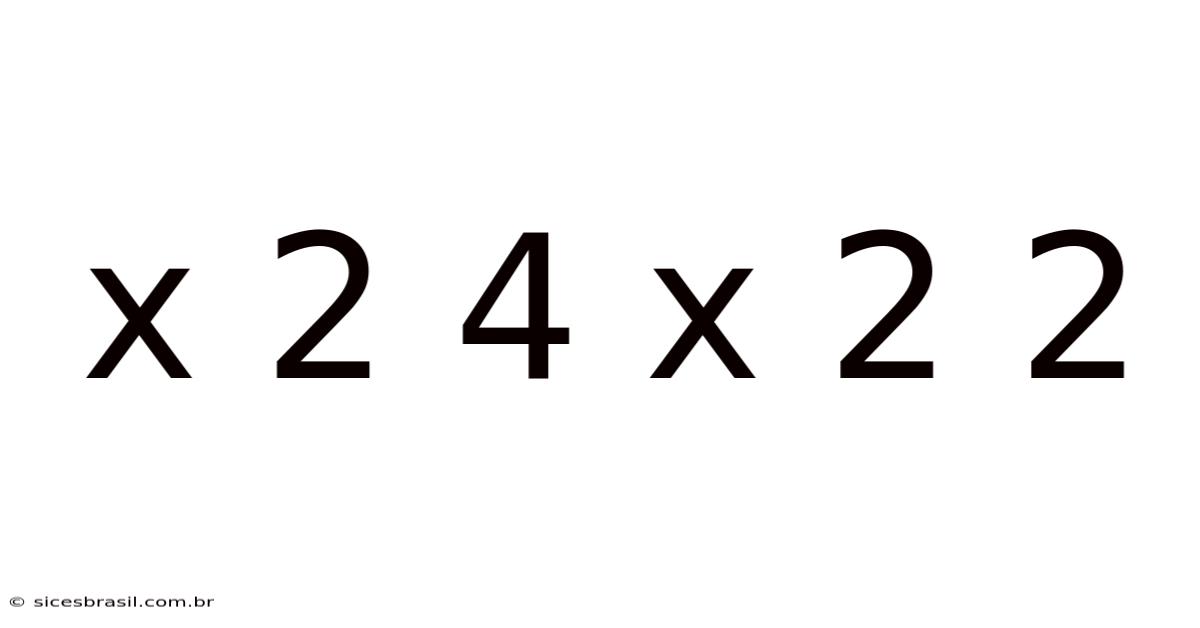
Table of Contents
Decoding the Mystery: A Deep Dive into x² + 4x + 2 = 0
This article explores the quadratic equation x² + 4x + 2 = 0, providing a comprehensive guide to understanding, solving, and interpreting its solutions. We'll journey from basic concepts to advanced techniques, ensuring a thorough grasp of this fundamental mathematical problem. This exploration will cover various methods of solving quadratic equations, the significance of the discriminant, and the real-world applications of such equations. Understanding quadratic equations is crucial for various fields, from physics and engineering to economics and finance.
Introduction: Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually x) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a ≠ 0. Our focus, x² + 4x + 2 = 0, fits this form with a = 1, b = 4, and c = 2. These equations represent curves called parabolas when graphed. Solving a quadratic equation means finding the values of x that make the equation true – these values are called the roots or solutions of the equation.
Methods for Solving Quadratic Equations
Several methods exist for solving quadratic equations. Let's examine the most common ones, applying them to our specific equation, x² + 4x + 2 = 0.
1. Factoring: This method involves rewriting the equation as a product of two linear expressions. Unfortunately, x² + 4x + 2 = 0 cannot be easily factored using integer coefficients. While some quadratic equations yield easily factorable expressions, many, like this one, do not.
2. Quadratic Formula: This is a powerful and universally applicable method. The quadratic formula provides the solutions for any quadratic equation in the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 4, c = 2), we get:
x = [-4 ± √(4² - 4 * 1 * 2)] / (2 * 1) x = [-4 ± √(16 - 8)] / 2 x = [-4 ± √8] / 2 x = [-4 ± 2√2] / 2 x = -2 ± √2
Therefore, the two solutions are x = -2 + √2 and x = -2 - √2. These are the exact solutions. Approximate values are x ≈ -0.586 and x ≈ -3.414.
3. Completing the Square: This method involves manipulating the equation to create a perfect square trinomial.
x² + 4x + 2 = 0 x² + 4x = -2 To complete the square, we take half of the coefficient of x (which is 4/2 = 2), square it (2² = 4), and add it to both sides:
x² + 4x + 4 = -2 + 4 (x + 2)² = 2 Taking the square root of both sides: x + 2 = ±√2 x = -2 ± √2
This yields the same solutions as the quadratic formula, demonstrating the equivalence of the methods.
The Significance of the Discriminant (b² - 4ac)
The expression b² - 4ac, found under the square root in the quadratic formula, is called the discriminant. It reveals important information about the nature of the roots:
- b² - 4ac > 0: The equation has two distinct real roots. This is the case for our equation (16 - 8 = 8 > 0).
- b² - 4ac = 0: The equation has one real root (a repeated root).
- b² - 4ac < 0: The equation has two complex roots (involving imaginary numbers).
In our case, the discriminant is positive, indicating two distinct real roots, which we've already calculated.
Graphical Representation and Interpretation
The equation x² + 4x + 2 = 0 represents a parabola. The x-intercepts of this parabola correspond to the roots of the equation. Graphing the parabola visually confirms the existence of two distinct x-intercepts, reinforcing our calculated solutions. The parabola opens upwards because the coefficient of x² (a = 1) is positive. The vertex of the parabola represents the minimum value of the quadratic function. We can find the x-coordinate of the vertex using the formula -b/2a = -4/(2*1) = -2. Substituting this back into the equation gives the y-coordinate: (-2)² + 4(-2) + 2 = -2. Thus, the vertex is at (-2, -2).
Real-World Applications of Quadratic Equations
Quadratic equations appear frequently in various fields:
- Physics: Projectile motion calculations often involve quadratic equations to determine the trajectory and time of flight of an object.
- Engineering: Designing bridges, buildings, and other structures often requires solving quadratic equations to ensure stability and strength.
- Economics: Quadratic functions can model supply and demand curves, profit maximization, and other economic phenomena.
- Computer Graphics: Parabolas, represented by quadratic equations, are essential in creating curved shapes and animation.
Frequently Asked Questions (FAQ)
Q: Can all quadratic equations be solved using factoring?
A: No. While some quadratic equations factor easily, many do not factor neatly using integer coefficients. The quadratic formula provides a reliable method for solving all quadratic equations.
Q: What if the discriminant is negative?
A: If the discriminant (b² - 4ac) is negative, the quadratic equation has two complex roots. These roots involve the imaginary unit i, where i² = -1. These complex roots have real and imaginary components.
Q: What is the practical significance of finding the vertex of the parabola?
A: The vertex represents either the maximum or minimum value of the quadratic function, depending on whether the parabola opens upwards (a > 0) or downwards (a < 0). This is crucial in optimization problems, such as finding the maximum profit or minimum cost.
Conclusion: Mastering Quadratic Equations
Solving x² + 4x + 2 = 0, using the quadratic formula, completing the square, and understanding the significance of the discriminant, provides a solid foundation in solving quadratic equations. This fundamental concept underpins numerous applications across diverse disciplines. Remember, the journey to mastering mathematics involves persistence and practice. By understanding the underlying principles and applying different solution methods, you can confidently tackle more complex mathematical challenges. The exploration of this seemingly simple equation has opened doors to broader mathematical concepts and their real-world implications. Continue your learning journey with confidence!
Latest Posts
Related Post
Thank you for visiting our website which covers about X 2 4 X 2 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.