What Percentage Of 12 Is 8
sicesbrasil
Sep 22, 2025 · 5 min read
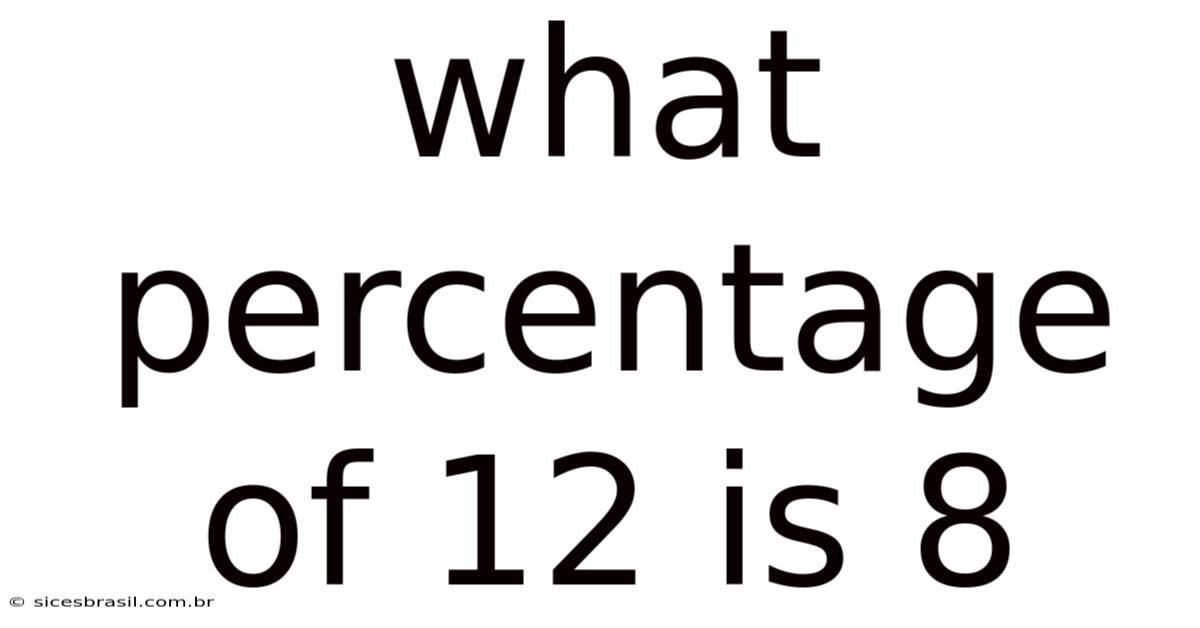
Table of Contents
What Percentage of 12 is 8? Understanding Percentages and Their Applications
This article delves into the seemingly simple question: "What percentage of 12 is 8?" While the calculation itself is straightforward, understanding the underlying principles of percentages and their wide-ranging applications is crucial. We'll explore the method of calculating percentages, delve into the mathematical reasoning, and showcase the relevance of percentage calculations in various real-world scenarios. This will equip you not only to solve this specific problem but also to confidently tackle similar percentage-related questions.
Understanding Percentages: A Foundational Concept
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10. Percentages are used extensively in various fields, including finance, statistics, science, and everyday life, to represent proportions, ratios, and changes.
Calculating "What Percentage of 12 is 8?"
To determine what percentage of 12 is 8, we follow these steps:
-
Set up a proportion: We can represent the problem as a proportion: 8/12 = x/100, where 'x' represents the unknown percentage.
-
Cross-multiply: Cross-multiplying the proportion gives us: 12x = 800
-
Solve for x: Divide both sides of the equation by 12: x = 800/12 = 66.666...
-
Round to the desired precision: We typically round percentages to two decimal places. Therefore, 8 is approximately 66.67% of 12.
Therefore, the answer to "What percentage of 12 is 8?" is approximately 66.67%.
The Mathematical Reasoning Behind Percentage Calculations
The method above relies on the fundamental principle of proportions. A proportion is a statement of equality between two ratios. In the context of percentages, one ratio represents the part (in this case, 8) to the whole (12), and the other ratio represents the percentage (x) to 100. Cross-multiplication, a technique used to solve proportions, ensures that the ratios remain equivalent.
Alternative Methods for Calculating Percentages
While the proportion method is widely used, there are other ways to calculate percentages:
-
Using decimals: We can express the fraction 8/12 as a decimal by dividing 8 by 12: 8 ÷ 12 = 0.666... To convert this decimal to a percentage, we multiply by 100: 0.666... × 100 ≈ 66.67%.
-
Using a calculator: Most calculators have a percentage function (%) that simplifies the calculation. You would enter 8 ÷ 12 = and then press the % button, which directly provides the percentage.
Choosing the method depends on personal preference and the tools available. However, understanding the underlying principles remains key.
Real-World Applications of Percentage Calculations
Percentage calculations are vital in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profits, and losses all involve percentages. For instance, understanding the percentage increase or decrease in your investments is crucial for financial planning.
-
Statistics: Percentages are used to represent data in charts, graphs, and summaries. They help visualize proportions and trends within datasets, facilitating informed decision-making.
-
Science: In scientific experiments and research, percentages are used to express concentrations, error margins, and the effectiveness of treatments. Understanding these percentages is critical for interpreting scientific findings.
-
Everyday life: Calculating tips in restaurants, figuring out sale prices, or determining the percentage of a task completed all require percentage calculations. These seemingly small calculations often play a significant role in our daily lives.
-
Education: Calculating grades, assessing test performance, and understanding student progress frequently rely on percentage calculations. Teachers use percentages to communicate student achievements effectively.
Beyond the Basics: More Complex Percentage Problems
While the question "What percentage of 12 is 8?" is relatively straightforward, percentage problems can become more complex. Consider the following examples:
-
Finding the percentage increase or decrease: Determining the percentage change between two values requires subtracting the initial value from the final value, dividing the result by the initial value, and then multiplying by 100.
-
Calculating percentages of percentages: This involves applying multiple percentage calculations sequentially, such as finding 20% of 15% of a certain value.
-
Working with complex proportions: Problems involving multiple parts and wholes may require more sophisticated proportional reasoning.
Frequently Asked Questions (FAQ)
-
Q: Can I use a different method to calculate the percentage? A: Yes, you can use decimals or a calculator with a percentage function as alternative methods. The choice depends on your preference and the tools at your disposal.
-
Q: What if the numbers are not whole numbers? A: The same principles apply. You can use fractions or decimals to perform the calculations, just as with whole numbers.
-
Q: What if I need to find the percentage of a larger number? A: The same approach applies. You will still set up a proportion and solve for the unknown percentage.
-
Q: How accurate should my answer be? A: The level of accuracy needed depends on the context. For most everyday situations, rounding to two decimal places is sufficient. However, in scientific or financial applications, higher precision might be necessary.
Conclusion: Mastering Percentages for a Broader Understanding
Understanding percentages is fundamental to navigating many aspects of life. While the calculation of "What percentage of 12 is 8?" may seem simple, grasping the underlying principles allows you to tackle more complex percentage-related problems. The ability to perform accurate percentage calculations is a valuable skill that empowers informed decision-making across various domains. By mastering this concept, you not only answer specific questions but also gain a broader understanding of proportions, ratios, and their applications in the real world. This empowers you to confidently analyze data, interpret information, and solve problems in a multitude of contexts, enhancing both your personal and professional capabilities. Remember that consistent practice is key to mastering percentage calculations and applying them effectively in diverse scenarios.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percentage Of 12 Is 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.