What Percent Of 42 Is 29.4
sicesbrasil
Sep 23, 2025 · 5 min read
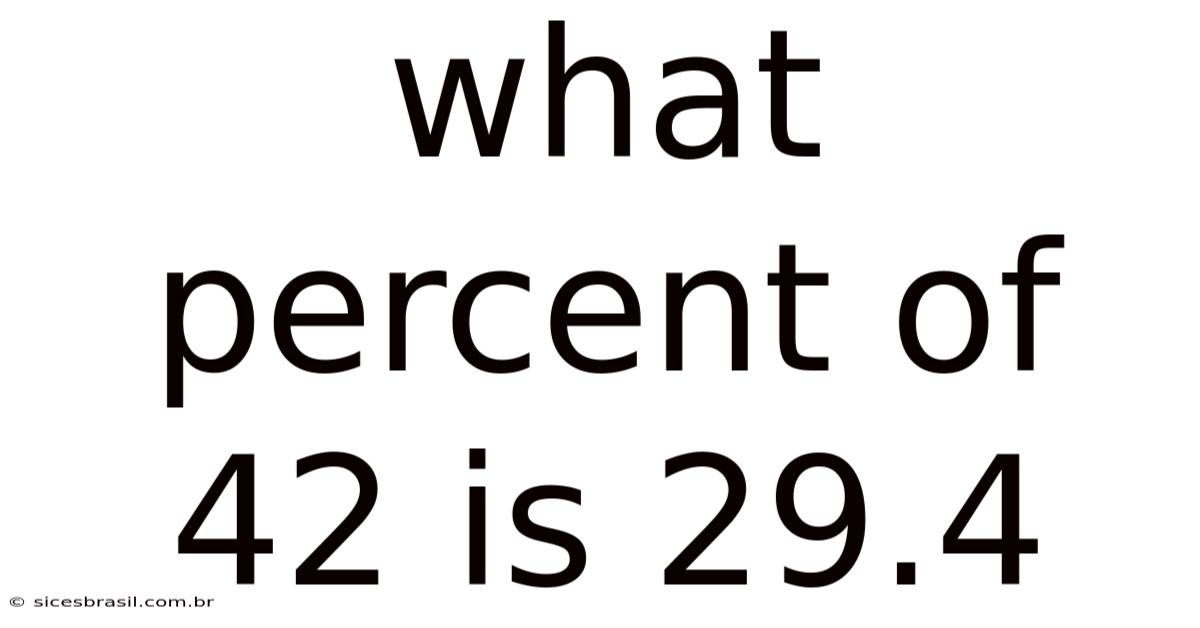
Table of Contents
What Percent of 42 is 29.4? A Deep Dive into Percentage Calculations
Finding what percent one number is of another is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and tax rates to understanding statistical data and analyzing financial reports. This article will not only answer the question "What percent of 42 is 29.4?" but will also provide a comprehensive understanding of percentage calculations, including different methods, real-world examples, and troubleshooting common mistakes. We will explore the underlying principles, ensuring you can confidently tackle similar problems in the future.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred" (per centum in Latin). It's a way of expressing a proportion or a part of a whole. For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Calculating the Percentage: Method 1 - The Proportion Method
This method uses the concept of ratios and proportions to solve percentage problems. We can set up a proportion to find the unknown percentage. The proportion will look like this:
Part / Whole = Percentage / 100
In our case:
Part = 29.4 Whole = 42 Percentage = x (this is what we want to find)
Substituting these values into the proportion, we get:
29.4 / 42 = x / 100
To solve for x, we can cross-multiply:
29.4 * 100 = 42 * x
2940 = 42x
Now, divide both sides by 42:
x = 2940 / 42
x = 70
Therefore, 29.4 is 70% of 42.
Calculating the Percentage: Method 2 - The Decimal Method
This method involves converting the fraction representing the part to a decimal and then multiplying by 100 to express it as a percentage.
First, we express the relationship between the part and the whole as a fraction:
29.4 / 42
Next, we convert this fraction to a decimal by dividing 29.4 by 42:
29.4 ÷ 42 = 0.7
Finally, we multiply the decimal by 100 to express it as a percentage:
0.7 * 100 = 70%
Again, we arrive at the answer: 29.4 is 70% of 42.
Why These Methods Work: A Deeper Look
Both methods are based on the fundamental principle of expressing a part as a fraction of a whole. The proportion method explicitly uses this fractional relationship, while the decimal method implicitly does so by first converting the fraction to a decimal. The multiplication by 100 in the decimal method is simply a conversion factor to express the decimal fraction as a percentage – a number out of 100.
Real-World Applications
Understanding percentage calculations is crucial in various real-world situations:
- Sales and Discounts: Calculating discounts offered on products. For example, if a $100 item is discounted by 20%, the discount amount is 20% of $100, which is $20.
- Taxes and Tips: Determining the tax amount on purchases or calculating the tip amount in a restaurant.
- Financial Analysis: Analyzing financial statements, such as profit margins and growth rates. Percentage changes help visualize trends and comparisons.
- Statistics and Probability: Expressing probabilities and proportions in statistical data. For example, the percentage of people who prefer a certain product.
- Grade Calculation: Calculating your final grade in a course based on individual assignment scores.
Troubleshooting Common Mistakes
Several common mistakes can occur when calculating percentages:
- Incorrectly identifying the part and the whole: Make sure you clearly identify which number represents the part and which represents the whole before starting the calculation.
- Errors in decimal calculations: When using the decimal method, double-check your division and multiplication to avoid errors in decimal places. Using a calculator can help minimize this.
- Misinterpreting the percentage: Always remember that the percentage represents a proportion out of 100.
- Confusing percentage increase and decrease: These involve different calculations. Percentage increase calculates the percentage change from a smaller to a larger value, while percentage decrease calculates the percentage change from a larger to a smaller value.
Expanding Your Understanding: Further Exploration
While we’ve solved the specific problem of determining what percent of 42 is 29.4, it’s beneficial to expand your understanding by considering related problems:
- Finding the part: If you know the whole and the percentage, you can calculate the part. For example, what is 70% of 42?
- Finding the whole: If you know the part and the percentage, you can calculate the whole. For example, if 70% of a number is 29.4, what is the number?
- Percentage change: Calculating percentage increase or decrease between two numbers.
Mastering percentage calculations involves understanding the underlying principles and practicing different types of percentage problems. The more you practice, the more confident you'll become.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve percentage problems?
A: Absolutely! Calculators are a great tool for performing the necessary divisions and multiplications accurately and efficiently. However, understanding the underlying principles is still essential to set up the problem correctly.
Q: What if the numbers are not whole numbers?
A: The methods described above work perfectly well with decimal numbers, as demonstrated in our example.
Q: How can I improve my understanding of percentages?
A: Practice regularly with different types of percentage problems. Start with simple examples and gradually work your way up to more complex ones. You can find many practice problems online or in textbooks.
Conclusion
Determining what percent of 42 is 29.4 involves applying the fundamental principles of percentage calculations. Whether you use the proportion method or the decimal method, both lead to the correct answer: 70%. Understanding percentages is a crucial skill with wide-ranging applications in numerous aspects of life. By mastering these methods and understanding the underlying concepts, you'll be equipped to confidently tackle various percentage-related problems and apply this valuable skill in your everyday life and academic pursuits. Remember to practice regularly to solidify your understanding and build your confidence in tackling these types of calculations.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 42 Is 29.4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.