What Percent Of 15 Is 9
sicesbrasil
Sep 22, 2025 · 5 min read
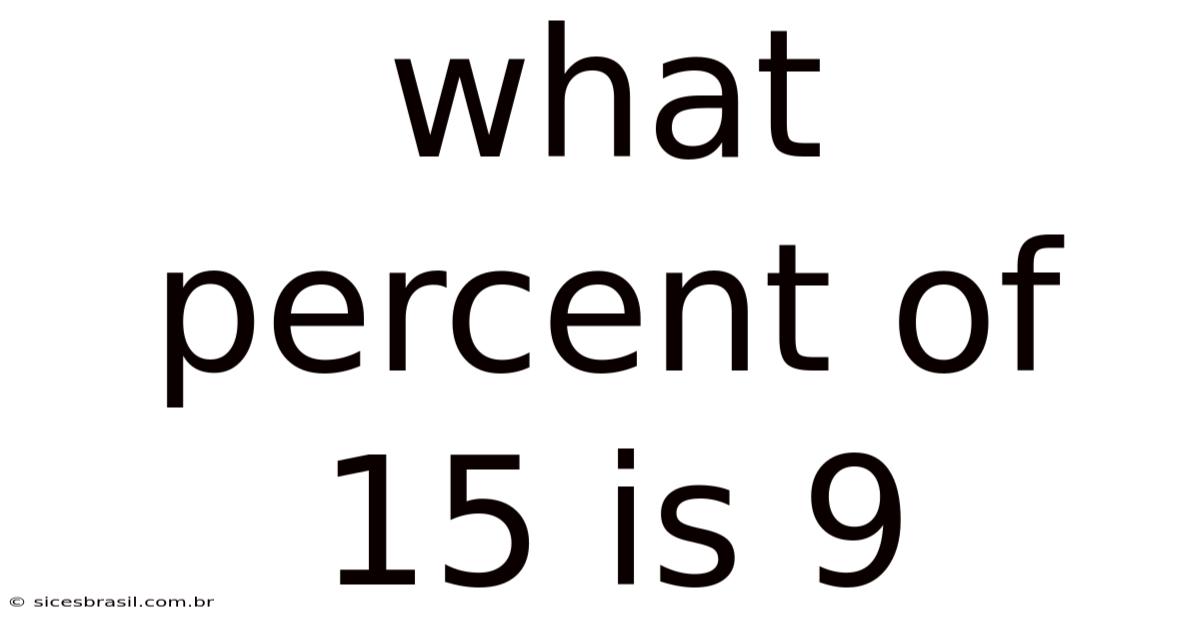
Table of Contents
What Percent of 15 is 9? Unlocking the World of Percentages
Finding what percentage one number represents of another is a fundamental skill in mathematics, crucial for various applications in everyday life, from calculating discounts and taxes to understanding statistics and analyzing data. This article will delve into the question: "What percent of 15 is 9?" We'll explore not only the solution but also the underlying concepts, different methods of solving percentage problems, and real-world applications. Understanding percentages allows you to confidently tackle similar problems and builds a stronger foundation in mathematical reasoning.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent" or "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used extensively to express proportions, changes, and rates.
Method 1: Setting up a Proportion
One of the most straightforward methods to solve percentage problems is to set up a proportion. A proportion is an equation stating that two ratios are equal. In our case, we want to find the percentage x such that x% of 15 is equal to 9. We can set up the following proportion:
x/100 = 9/15
This equation reads: "x out of 100 is equal to 9 out of 15." To solve for x, we can cross-multiply:
15x = 900
Now, divide both sides by 15:
x = 900 / 15
x = 60
Therefore, 9 is 60% of 15.
Method 2: Using the Formula
Another effective approach involves using the percentage formula:
Percentage = (Part / Whole) * 100
In our problem:
- Part: 9 (the number we want to express as a percentage)
- Whole: 15 (the total number)
Substituting these values into the formula:
Percentage = (9 / 15) * 100
Percentage = 0.6 * 100
Percentage = 60
Again, we find that 9 is 60% of 15.
Method 3: Decimal Conversion
This method involves converting the fraction representing the part to a decimal and then multiplying by 100 to express it as a percentage.
First, express the relationship as a fraction: 9/15
Then, simplify the fraction: 9/15 = 3/5
Now, convert the simplified fraction into a decimal by dividing the numerator by the denominator: 3 ÷ 5 = 0.6
Finally, multiply the decimal by 100 to express it as a percentage: 0.6 * 100 = 60%
Thus, 9 is 60% of 15.
Illustrative Examples: Real-World Applications
Let's explore how understanding percentages, and specifically solving problems like "What percent of 15 is 9?", can be applied in practical situations:
-
Sales and Discounts: A store offers a discount on an item originally priced at $15. If the discounted price is $9, the discount percentage can be calculated using the methods described above. The discount is 60%.
-
Grade Calculation: A student scores 9 points out of a possible 15 points on a quiz. Their percentage score is 60%. This helps evaluate their performance relative to the maximum possible score.
-
Data Analysis: In statistical analysis, percentages are frequently used to represent proportions within a dataset. For instance, if 9 out of 15 respondents answered "yes" to a survey question, 60% of the respondents answered affirmatively.
-
Financial Calculations: Understanding percentages is crucial for managing personal finances. Calculating interest rates, taxes, and investment returns all involve percentage calculations.
Further Exploration: Variations and Extensions
The fundamental concept behind calculating percentages can be extended to more complex scenarios. Consider these variations:
-
Finding the Whole: If we know that 60% of a number is 9, we can reverse the process to find the whole number. We'd set up the equation: 0.6x = 9, and solve for x, which would equal 15.
-
Finding the Part: If we know a percentage and the whole, we can find the part. For example, what is 60% of 15? This is simply 0.6 * 15 = 9.
-
Percentage Increase/Decrease: These calculations involve finding the percentage change between two numbers. For example, if a quantity increases from 15 to 21, the percentage increase is calculated as [(21-15)/15] * 100 = 40%.
Frequently Asked Questions (FAQ)
Q: What is the easiest method to calculate percentages?
A: The method that feels easiest depends on individual preferences. However, setting up a proportion is often a straightforward approach, especially for beginners. The formula method is also efficient once you're comfortable with the equation.
Q: Can I use a calculator to solve percentage problems?
A: Yes, calculators can greatly simplify the process. Most calculators have a percentage function (%) that can be used directly or you can perform the calculation manually using the decimal representation.
Q: Why are percentages important?
A: Percentages provide a standardized way to compare different quantities, making it easy to understand proportions and make informed decisions in various aspects of life.
Q: What if the numbers aren't whole numbers?
A: The methods described work equally well with decimals or fractions. Simply apply the same principles of setting up a proportion or using the formula.
Conclusion
This in-depth exploration demonstrates that calculating what percent of 15 is 9 is a straightforward process with multiple solution paths. Mastering percentage calculations is essential for numerous real-world applications, from everyday budgeting to advanced statistical analysis. By understanding the underlying concepts and employing the different methods discussed here, you can confidently tackle similar percentage problems and improve your mathematical proficiency. Remember, practice is key – the more you work with percentage problems, the more intuitive and easy they will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Of 15 Is 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.