What Percent Is 10 Of 25
sicesbrasil
Sep 24, 2025 · 5 min read
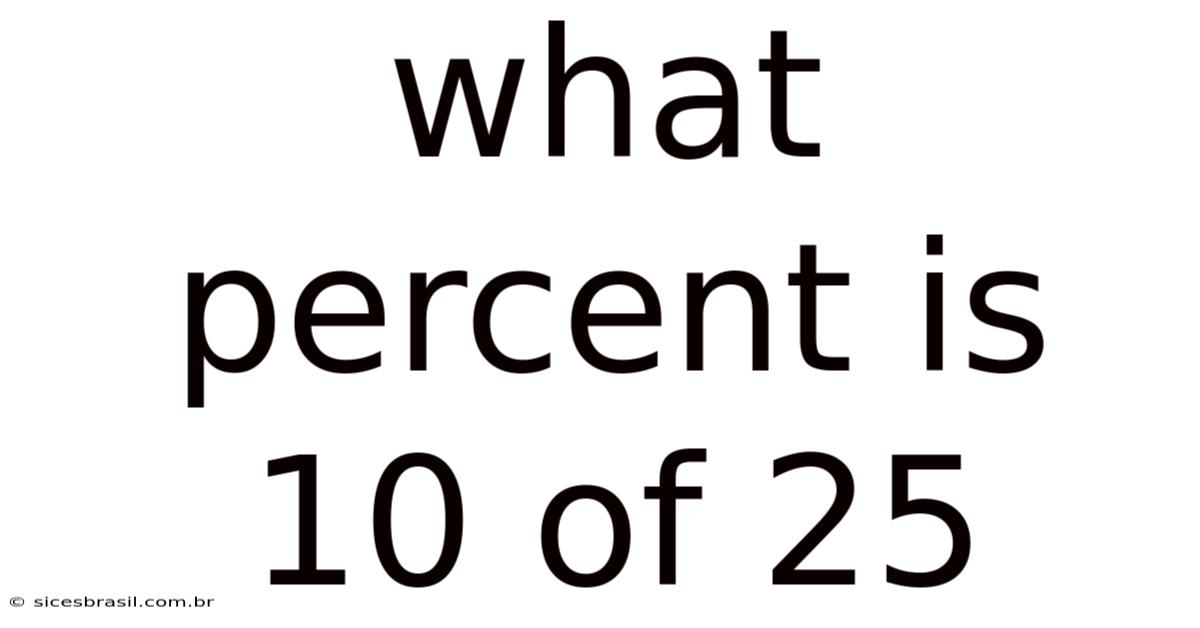
Table of Contents
What Percent is 10 of 25? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with widespread applications in daily life, from calculating discounts and sales tax to understanding statistics and financial reports. This article will thoroughly explore the question, "What percent is 10 of 25?", providing not only the answer but also a comprehensive understanding of the underlying concepts and methods involved in percentage calculations. We'll delve into different approaches, including using proportions, fractions, and the basic percentage formula, ensuring you gain a solid grasp of this essential mathematical concept.
Understanding Percentages: A Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The word "percent" literally means "per hundred" or "out of 100." When we say 10% (ten percent), we mean 10 out of every 100. This can be represented as a fraction (10/100), a decimal (0.10), or, as we will be exploring, as part of a larger whole. Understanding this fundamental concept is crucial for solving percentage problems.
Method 1: Using Proportions to Find the Percentage
Proportions offer a clear and logical way to solve percentage problems. A proportion is an equation stating that two ratios are equal. In our case, we can set up a proportion to find what percentage 10 represents out of 25.
We can represent this as:
10/25 = x/100
Where:
- 10 represents the part.
- 25 represents the whole.
- x represents the unknown percentage we are trying to find.
- 100 represents the total percentage (100%).
To solve for x, we cross-multiply:
10 * 100 = 25 * x
1000 = 25x
Now, divide both sides by 25:
x = 1000 / 25
x = 40
Therefore, 10 is 40% of 25.
Method 2: Converting to a Fraction and then a Percentage
Another effective approach is to convert the given numbers into a fraction and then into a percentage.
First, express the relationship between the part (10) and the whole (25) as a fraction:
10/25
Next, simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 5:
10/25 = 2/5
Now, to convert this fraction into a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by 20 (since 5 * 20 = 100):
(2 * 20) / (5 * 20) = 40/100
Since 40/100 represents 40 out of 100, this is equivalent to 40%.
Method 3: Using the Percentage Formula
The basic percentage formula provides a direct method for solving percentage problems. The formula is:
Percentage = (Part / Whole) * 100
Let's apply this to our problem:
Percentage = (10 / 25) * 100
Percentage = 0.4 * 100
Percentage = 40
Therefore, 10 is 40% of 25.
Expanding on Percentage Concepts: Beyond the Basics
While we've successfully determined that 10 is 40% of 25, understanding the broader context of percentage calculations is vital for applying this knowledge effectively in various situations. Let's explore some related concepts:
-
Finding the Part: If you know the percentage and the whole, you can find the part. For example, what is 20% of 50? The formula becomes: Part = (Percentage/100) * Whole. So, Part = (20/100) * 50 = 10.
-
Finding the Whole: If you know the percentage and the part, you can find the whole. For instance, if 15 is 30% of a number, what is that number? The formula is rearranged as: Whole = (Part * 100) / Percentage. So, Whole = (15 * 100) / 30 = 50.
-
Percentage Increase/Decrease: Percentage changes are frequently encountered in real-world applications. A percentage increase is calculated as: [(New Value - Old Value) / Old Value] * 100. A percentage decrease is calculated similarly but with a negative result.
-
Compound Interest: This is a crucial concept in finance where interest earned is added to the principal, and subsequent interest is calculated on the accumulated amount. Understanding compound interest involves repeated percentage calculations.
-
Statistical Analysis: Percentages play a significant role in statistical analysis, helping to interpret data and draw meaningful conclusions from large datasets.
Practical Applications of Percentage Calculations
The ability to calculate percentages accurately has numerous practical applications across various fields:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
-
Retail: Determining sale prices, markups, and discounts.
-
Science: Representing experimental data, statistical analysis, and measurements.
-
Everyday Life: Calculating tips, splitting bills, and understanding proportions in recipes.
Frequently Asked Questions (FAQ)
Q1: What if I want to calculate a different percentage?
A1: The methods described above can be applied to any percentage calculation. Simply replace the numbers with the values relevant to your problem and follow the steps.
Q2: Are there any shortcuts for calculating percentages mentally?
A2: Yes, several mental math tricks can simplify percentage calculations. For example, finding 10% is simply dividing the number by 10. 5% is half of 10%, and so on. Practicing these shortcuts can improve your speed and accuracy.
Q3: What are some common mistakes to avoid when calculating percentages?
A3: Common mistakes include: incorrectly setting up the proportion, misinterpreting the problem's context, and making errors in arithmetic. Careful attention to detail and a systematic approach can help avoid these mistakes.
Q4: What are some resources for further learning about percentages?
A4: Many online resources, educational websites, and textbooks provide comprehensive explanations and practice problems on percentages and other mathematical concepts.
Conclusion: Mastering Percentage Calculations
This article has provided a detailed explanation of how to calculate what percent 10 is of 25, using multiple methods. More importantly, it has aimed to build a strong foundation in understanding percentages, their applications, and related concepts. Mastering percentage calculations is not just about knowing the formulas; it's about developing a conceptual understanding that allows you to apply these skills confidently and accurately in diverse situations. Whether you are a student grappling with math problems, a professional dealing with financial data, or simply someone who wants to improve their numeracy skills, understanding percentages is a valuable asset. Practice regularly, explore different methods, and you’ll soon find percentage calculations become second nature.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Percent Is 10 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.