What Is Half Of 3/2
sicesbrasil
Sep 22, 2025 · 5 min read
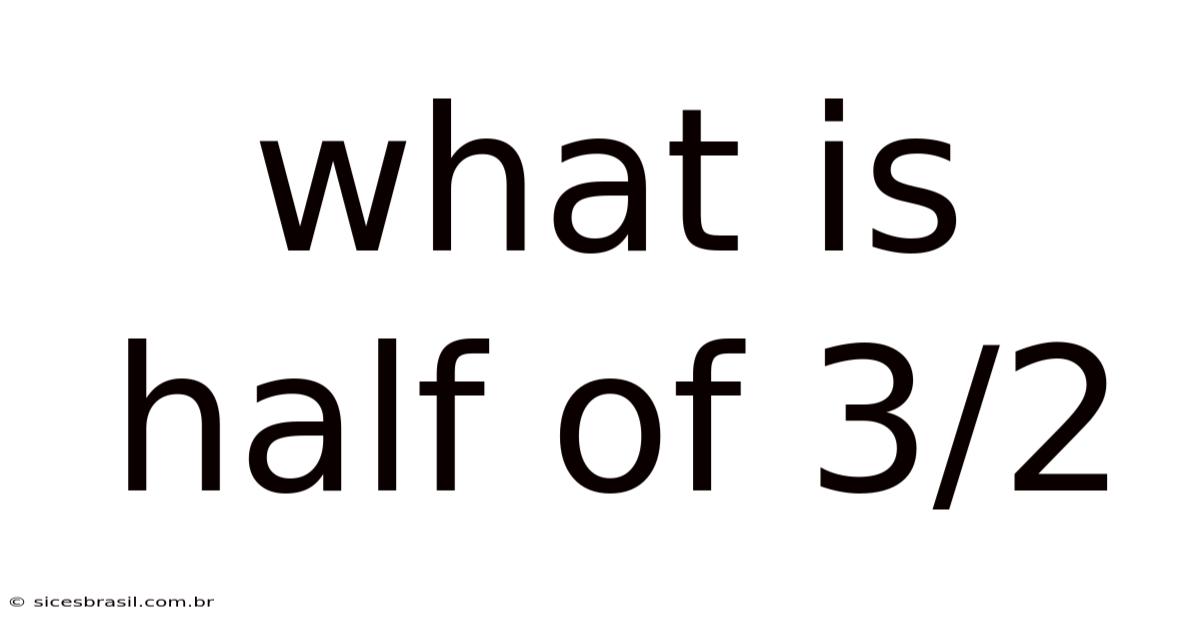
Table of Contents
What is Half of 3/2? A Deep Dive into Fractions and Division
Finding half of 3/2 might seem like a simple arithmetic problem, but it offers a fantastic opportunity to explore fundamental concepts in mathematics, particularly fractions and division. This article will not only provide the answer but also delve into the underlying principles, providing a comprehensive understanding for learners of all levels. We'll cover various methods for solving this problem, exploring different approaches to fraction manipulation and reinforcing crucial mathematical skills.
Introduction: Understanding Fractions
Before we tackle the problem of finding half of 3/2, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/2, 3 is the numerator and 2 is the denominator. This means we have 3 parts of a whole that's divided into 2 equal parts. Notice that 3/2 is an improper fraction because the numerator is larger than the denominator. This indicates a value greater than 1.
Method 1: Converting to a Mixed Number
One way to approach finding half of 3/2 is to first convert the improper fraction into a mixed number. A mixed number combines a whole number and a proper fraction (where the numerator is smaller than the denominator). To convert 3/2 to a mixed number, we divide the numerator (3) by the denominator (2):
3 ÷ 2 = 1 with a remainder of 1.
This means 3/2 is equal to 1 and 1/2. Now, finding half of 1 and 1/2 is easier to visualize. Half of 1 is 1/2, and half of 1/2 is 1/4. Adding these together, we get:
1/2 + 1/4 = 2/4 + 1/4 = 3/4
Therefore, half of 3/2 is 3/4.
Method 2: Direct Multiplication by 1/2
Another, perhaps more efficient, method involves directly multiplying 3/2 by 1/2. Remember that "half of" means multiplying by 1/2. Multiplying fractions involves multiplying the numerators together and the denominators together:
(3/2) * (1/2) = (3 * 1) / (2 * 2) = 3/4
This method directly confirms that half of 3/2 is indeed 3/4.
Method 3: Visual Representation
Visualizing the problem can aid understanding. Imagine a circle divided into two equal halves. 3/2 means we have one whole circle and another half-circle. To find half of this, we divide the whole circle into two halves and the half-circle into two quarters. This leaves us with three quarters of a circle, visually representing 3/4. This method is particularly useful for beginners to grasp the concept of fractions and division.
Explanation: The Mathematics Behind the Calculation
The success of these methods hinges on a strong understanding of fraction multiplication and division. When we multiply fractions, we are essentially finding a portion of a portion. Multiplying 3/2 by 1/2 means we are taking half of the quantity represented by 3/2. The result, 3/4, accurately reflects this operation.
The conversion to a mixed number simplifies the visualization, making it easier to comprehend the division process. Breaking down the mixed number (1 1/2) into its components and finding half of each part allows for a step-by-step approach to solving the problem, suitable for learners who might find direct fraction multiplication more challenging initially.
Extending the Concept: Working with More Complex Fractions
The principles demonstrated here can be applied to more complex fraction problems. For instance, finding a third of 5/6 would involve multiplying 5/6 by 1/3, resulting in 5/18. The key is to remember the fundamental rules of fraction multiplication and the intuitive meaning of taking a fraction of another fraction.
Frequently Asked Questions (FAQ)
Q1: Can I solve this using decimals?
A1: Yes, you can. First, convert 3/2 to a decimal: 3/2 = 1.5. Then, find half of 1.5: 1.5 / 2 = 0.75. Finally, convert 0.75 back to a fraction: 0.75 = 75/100 = 3/4. This method demonstrates the equivalence between fractions and decimals.
Q2: Why is it important to understand different methods for solving this problem?
A2: Using multiple methods strengthens your understanding of the underlying mathematical concepts. Different methods appeal to different learning styles, and mastering multiple approaches provides a more robust foundation in mathematics. It also enhances problem-solving skills and allows for flexibility in choosing the most efficient method for a given problem.
Q3: What if the fraction was negative?
A3: If the fraction were negative, for example, -3/2, the process remains the same, but the result would also be negative. Half of -3/2 is -3/4. Remember that multiplying a negative number by a positive number results in a negative number.
Q4: How can I practice more problems like this?
A4: Practice is crucial for mastering fractions. Create your own problems using various fractions, both proper and improper. Try different methods for each problem to solidify your understanding. You can also find numerous practice exercises online or in textbooks. Focus on understanding the process rather than just getting the answer.
Conclusion: Mastering Fractions, One Step at a Time
Finding half of 3/2, while seemingly simple, reveals a wealth of mathematical concepts. Through the exploration of different methods—converting to mixed numbers, direct multiplication, and visual representation—we have reinforced the principles of fraction manipulation and division. This problem serves as a stepping stone to tackling more complex fraction problems. By understanding the underlying principles and practicing regularly, you can build a strong foundation in mathematics and confidently approach increasingly challenging calculations. Remember, mastering fractions is a journey, and each problem solved brings you closer to mathematical fluency. The key is consistent practice and a focus on truly understanding the “why” behind the calculations, not just the “how.”
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is Half Of 3/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.