What Is 60/40 With 300 As The 60
sicesbrasil
Sep 23, 2025 · 6 min read
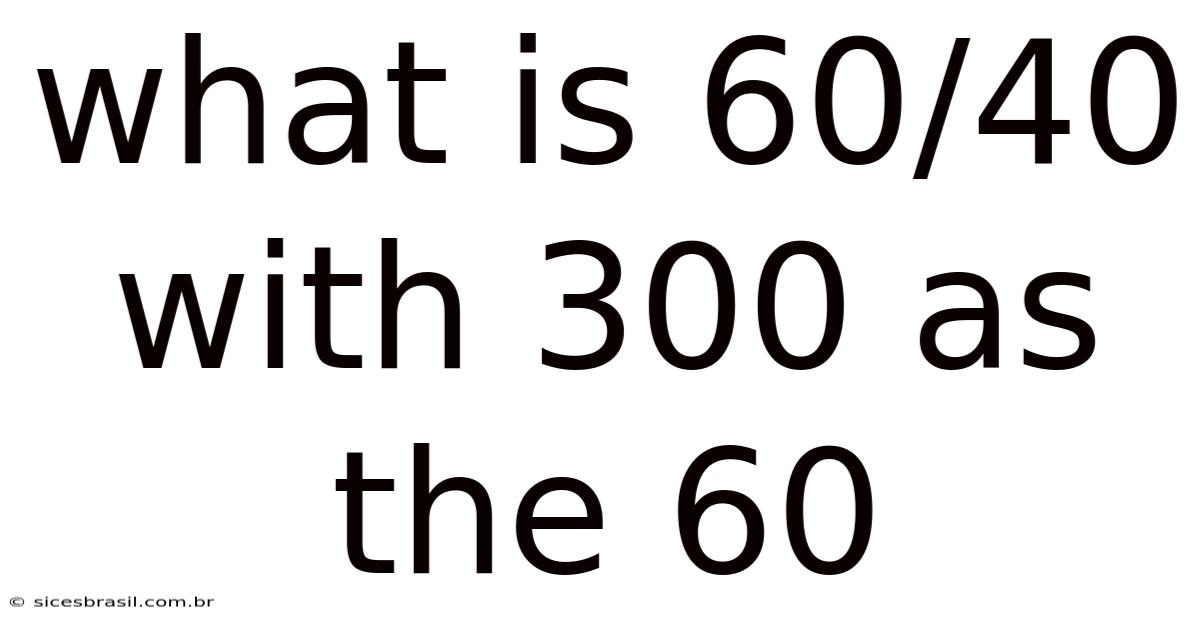
Table of Contents
Decoding the 60/40 Ratio: Understanding Proportions and Applications
Understanding ratios is a fundamental skill applicable across numerous fields, from basic mathematics to complex financial modeling. This article delves into the concept of a 60/40 ratio, specifically when 300 represents the 60% portion. We'll explore how to calculate the remaining 40%, examine real-world applications, and address common questions surrounding this type of proportional relationship. This comprehensive guide will equip you with the knowledge to confidently utilize and interpret 60/40 ratios in various contexts.
Understanding the 60/40 Ratio
A 60/40 ratio signifies a proportional relationship where one part represents 60% of the whole, and the other part represents the remaining 40%. In simpler terms, it's a division of a total quantity into two parts, with one part being 1.5 times larger than the other. This ratio is frequently encountered in finance, statistics, and everyday problem-solving.
In our specific scenario, we know that 300 represents the 60% portion. This provides a foundation for calculating the remaining 40% and the total value.
Calculating the 40% Portion
To determine the value representing the 40% portion, we can use several methods. The most straightforward approach involves utilizing proportions:
Method 1: Using Proportions
We can set up a proportion:
60/100 = 300/x
Where 'x' represents the total value. Solving for 'x':
60x = 30000
x = 500
Therefore, the total value is 500. Now, we can calculate the 40% portion:
40% of 500 = (40/100) * 500 = 200
So, the 40% portion is 200.
Method 2: Finding the Unit Value
Alternatively, we can find the value of 1% of the total and then multiply by 40:
If 300 represents 60%, then 1% would be:
300 / 60 = 5
Therefore, 40% would be:
5 * 40 = 200
Again, the 40% portion is 200.
Both methods yield the same result: if 300 represents 60% of a total, then the remaining 40% is 200, and the total is 500.
Real-World Applications of the 60/40 Ratio
The 60/40 ratio finds application in diverse fields:
-
Finance: A common investment strategy involves a 60/40 portfolio allocation. This means 60% of the investment is in stocks (equities) for growth potential, and 40% is in bonds for stability and lower risk. Adjusting this ratio depends on individual risk tolerance and investment goals. In this context, if a portfolio worth 300 units has 60% in equities, this signifies a 300 unit equity position, and the bond portion (40%) would be 200 units as calculated above.
-
Project Management: Project budgets or time allocation might follow a 60/40 ratio. For instance, 60% of the budget might be allocated to development, with the remaining 40% designated for marketing and launch. Similarly, project timelines can be divided proportionally. Consider a project with a 300-hour development phase, indicating that the remaining marketing and launch phase would be 200 hours.
-
Marketing and Sales: Marketing campaigns often allocate resources according to specific ratios. A 60/40 split might be used to divide spending between online and offline channels. If a company allocated $300,000 to online marketing representing 60% of their budget, the remaining $200,000 would be for offline marketing.
-
Recipe Scaling: Imagine a recipe calls for 300 grams of flour, representing 60% of the total dry ingredients. This allows you to calculate the remaining 40% (200 grams) needed to complete the recipe's dry ingredient list.
-
Data Analysis: In statistical analysis, data might be categorized into different groups following a 60/40 split. For instance, a sample of 300 participants might represent 60% of the total study population, indicating that the remainder of the population is 200 individuals.
These examples demonstrate the versatility of the 60/40 ratio across various domains. Its usefulness stems from its ability to represent a balanced approach, often incorporating both risk and stability, or growth and sustainability.
Mathematical Explanation and Further Applications
The 60/40 ratio is a simple representation of a percentage-based division. It can be expressed as a fraction (60/100 or 3/5 for 60%, and 40/100 or 2/5 for 40%) or as decimals (0.6 and 0.4 respectively). This foundational understanding facilitates the application of this ratio in various mathematical problems and real-world scenarios.
Beyond the basic calculations shown earlier, understanding this ratio allows for scalability. If the 60% portion changes, you can proportionally adjust the 40% portion. For example:
- If 60% = 600, then the total is 1000, and 40% = 400
- If 60% = 150, then the total is 250, and 40% = 100
These examples highlight the flexibility of the ratio. It’s not merely a fixed relationship but a proportional model adaptable to various scales.
This ratio can be incorporated into more complex mathematical models, such as linear equations or proportion problems. Consider problems involving concentrations, mixtures, or dilutions. Understanding the ratio allows for straightforward calculations related to the proportional amounts of different components.
Frequently Asked Questions (FAQs)
Q1: What if the 60% portion is not given as a whole number?
A1: The same principles apply. Let’s say 60% is represented by 300.5. You would follow the same steps as before, either using proportions or calculating the unit value of 1%. The calculations will involve decimals, but the process remains the same.
Q2: Are there other common ratios used in similar ways?
A2: Yes, many other ratios are commonly used, depending on the context. Common examples include 70/30, 80/20 (the Pareto Principle), 50/50, and various others. Each ratio represents a different proportional relationship. The principles of calculating the parts based on the given information remain consistent.
Q3: How does the 60/40 ratio relate to percentages?
A3: The 60/40 ratio is inherently a percentage-based representation. 60% and 40% together add up to 100%, representing the entirety of the whole. Understanding percentage calculations is crucial for working with this ratio.
Q4: Can the 60/40 ratio be applied to negative values?
A4: While the calculations can still be performed mathematically, the practical application of a 60/40 ratio to negative values needs careful consideration within the specific context. The concept of a portion being "larger" or "smaller" becomes less intuitive when dealing with negative quantities. It’s important to ensure the application aligns logically with the scenario.
Conclusion
The 60/40 ratio is a versatile tool with wide-ranging applicability. Understanding its underlying principles and application methods is crucial for solving problems across diverse fields. Whether you are managing a portfolio, analyzing data, or scaling a recipe, the ability to interpret and utilize this ratio effectively empowers you with problem-solving skills and a deeper understanding of proportions. Remember, the core concept is about understanding the proportional relationships and using that understanding to solve problems, regardless of the specific numerical values involved. The methods outlined in this article provide a solid foundation for confidently handling various situations involving this common and useful ratio.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 60/40 With 300 As The 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.