What Is 40 Of 120
sicesbrasil
Sep 22, 2025 · 5 min read
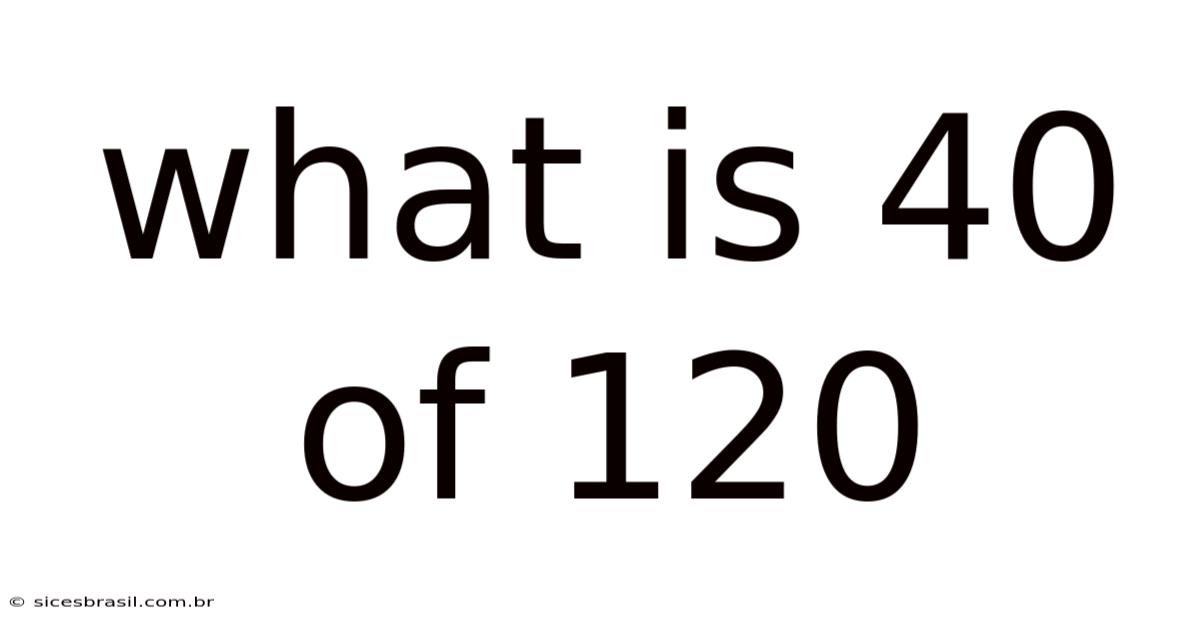
Table of Contents
What is 40 of 120? Understanding Percentages, Fractions, and Ratios
This article delves into the seemingly simple question: "What is 40 of 120?" While the immediate answer might seem obvious, exploring this question provides a fantastic opportunity to understand fundamental mathematical concepts like percentages, fractions, and ratios. These concepts are crucial for everyday life, from calculating discounts and tips to understanding financial reports and scientific data. We'll break down the calculation, explain the underlying principles, and explore related applications to solidify your understanding.
Understanding the Problem: 40 of 120
The phrase "40 of 120" implies a part-to-whole relationship. We want to determine what proportion 40 represents when compared to the total of 120. This can be expressed in several ways: as a fraction, a decimal, or a percentage. Each representation offers a unique perspective on the relationship between these two numbers.
Method 1: Calculating the Fraction
The most straightforward approach is to express the relationship as a fraction. The part (40) becomes the numerator, and the whole (120) becomes the denominator:
40/120
This fraction can be simplified by finding the greatest common divisor (GCD) of 40 and 120. The GCD is 40. Dividing both the numerator and denominator by 40, we get:
40 ÷ 40 / 120 ÷ 40 = 1/3
Therefore, 40 represents one-third (1/3) of 120.
Method 2: Calculating the Percentage
Percentages provide a standardized way to express proportions. To calculate the percentage, we first express the relationship as a fraction (as shown above): 40/120. Then, we convert this fraction to a decimal by dividing the numerator by the denominator:
40 ÷ 120 = 0.333...
This decimal represents the proportion of 40 to 120. To convert this decimal to a percentage, we multiply by 100:
0.333... × 100 = 33.33...%
Therefore, 40 represents approximately 33.33% of 120. The recurring decimal indicates that the percentage is not exactly 33.33%, but rather a repeating decimal infinitely close to this value.
Method 3: Using Ratios
Ratios offer another way to express the relationship between 40 and 120. A ratio shows the relative size of two or more values. In this case, the ratio is:
40:120
Similar to the fraction, we can simplify this ratio by dividing both numbers by their GCD (40):
40 ÷ 40 : 120 ÷ 40 = 1:3
This simplified ratio, 1:3, indicates that for every one part of 40, there are three parts of 120. This representation clearly shows the proportional relationship between the two numbers.
Expanding the Understanding: Applications and Real-World Examples
The principles illustrated by calculating "40 of 120" have widespread applications in numerous fields:
-
Business and Finance: Calculating profit margins, discounts, sales tax, and interest rates all rely on understanding percentages and ratios. For example, if a store offers a 33.33% discount on an item originally priced at $120, the discount amount would be $40.
-
Science and Engineering: Scientists and engineers frequently use ratios and percentages to analyze data, compare experimental results, and represent proportions in various contexts. For instance, determining the concentration of a solution or the efficiency of a machine often involves calculating percentages.
-
Everyday Life: Calculating tips in restaurants, determining the amount of ingredients needed for a recipe (based on scaling up or down), and understanding statistics related to weather, health, or sports all involve interpreting percentages, fractions, and ratios.
-
Data Analysis: Understanding proportions is crucial for interpreting data. For instance, if a survey shows that 40 out of 120 respondents prefer a certain product, this signifies a preference rate of approximately 33.33%.
Beyond the Basics: Further Exploration of Percentages, Fractions, and Ratios
While calculating "40 of 120" provides a basic introduction, delving deeper into the underlying concepts reveals their versatility and power:
-
Percentage Increase/Decrease: Understanding how to calculate percentage changes is crucial for analyzing trends and growth. For example, if a value increases from 40 to 120, the percentage increase is calculated as: [(120 - 40) / 40] x 100% = 200%.
-
Compound Interest: Compound interest calculations rely heavily on percentages and exponential growth. Understanding this concept is vital for making informed financial decisions regarding investments and loans.
-
Proportional Reasoning: Proportional reasoning involves understanding the relationships between different quantities and using this understanding to solve problems. This skill is extensively used in various mathematical and scientific applications.
-
Ratio and Proportion Problems: Solving problems involving ratios and proportions often involves setting up equations and solving for unknown variables. This is a fundamental skill in algebra and other branches of mathematics.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of the fraction 40/120?
- A: The simplest form is 1/3.
-
Q: Can I use a calculator to solve this?
- A: Yes, you can use a calculator to divide 40 by 120 to get the decimal value (0.333...), then multiply by 100 to get the percentage.
-
Q: Is there more than one way to solve this problem?
- A: Yes, as demonstrated, there are multiple approaches: using fractions, percentages, and ratios. Each approach provides a different perspective on the same relationship.
-
Q: What if the numbers were different? How would the approach change?
- A: The approach remains the same. You would always express the "part" as a fraction of the "whole," simplify the fraction if possible, and then convert it to a percentage or express it as a ratio as needed.
-
Q: How can I improve my understanding of percentages, fractions, and ratios?
- A: Practice solving various problems involving these concepts. Work through examples, use online resources and tutorials, and consider seeking help from a tutor or teacher if needed.
Conclusion: Mastering Fundamental Mathematical Concepts
The question "What is 40 of 120?" serves as a springboard to explore the fundamental concepts of percentages, fractions, and ratios. Mastering these concepts is not merely about solving mathematical problems; it's about developing a deeper understanding of proportional relationships and their application in diverse areas of life. By grasping these principles, you equip yourself with essential skills for critical thinking, problem-solving, and navigating the quantitative aspects of the world around you. Remember that practice is key to solidifying your understanding and building confidence in your mathematical abilities. Keep exploring, keep practicing, and keep learning!
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 40 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.