What Is 30 Of 7000
sicesbrasil
Sep 23, 2025 · 5 min read
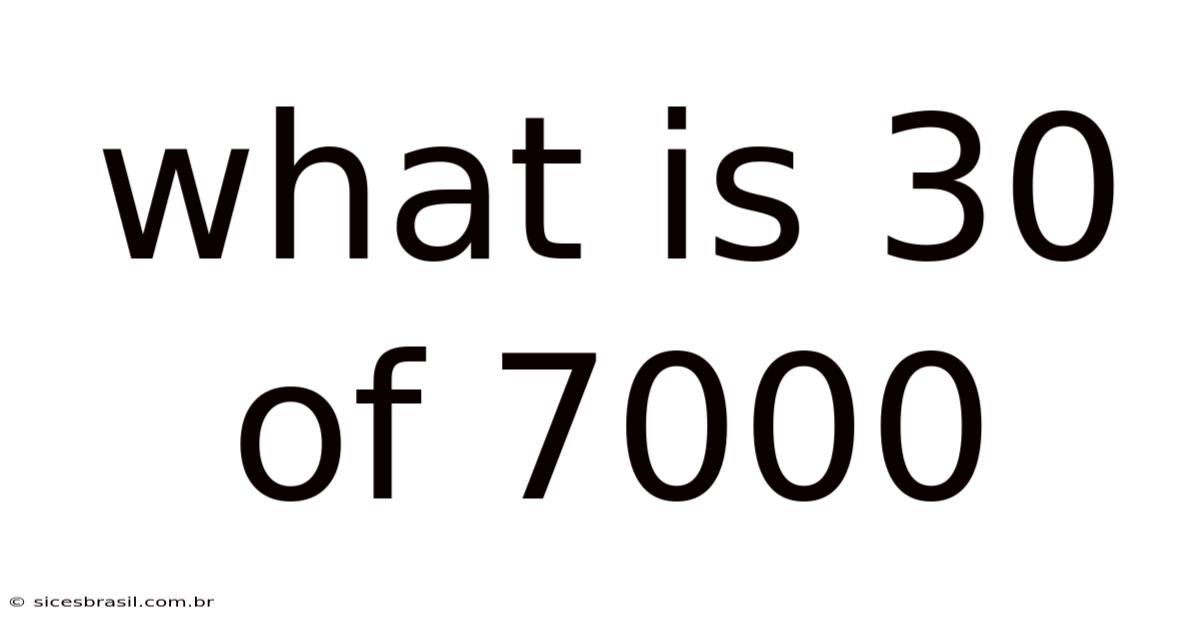
Table of Contents
What is 30/7000? Understanding Fractions, Decimals, and Percentages
This article delves into the seemingly simple question: "What is 30/7000?" But beyond simply providing the answer, we will explore the underlying mathematical concepts, demonstrating how to solve this problem and similar ones, and explaining the significance of representing numbers in different formats – fractions, decimals, and percentages. This exploration will enhance your understanding of fundamental mathematical principles and equip you with practical skills applicable in various contexts.
Introduction: Understanding Fractions
The expression "30/7000" represents a fraction. A fraction is a way of expressing a part of a whole. It consists of two parts:
- Numerator: The top number (30 in this case) represents the part we are interested in.
- Denominator: The bottom number (7000) represents the total number of parts that make up the whole.
Therefore, 30/7000 means 30 parts out of a total of 7000 parts. Understanding this fundamental concept is crucial for solving this problem and for tackling more complex fractional calculations in the future.
Calculating 30/7000: Step-by-Step
There are several ways to determine the value of 30/7000:
1. Simplification through Division:
The simplest approach is to simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both 30 and 7000 without leaving a remainder. In this case, the GCD of 30 and 7000 is 10. We can divide both the numerator and denominator by 10:
30 ÷ 10 = 3 7000 ÷ 10 = 700
This simplifies the fraction to 3/700. This simplified fraction is equivalent to the original fraction, meaning it represents the same value.
2. Converting to a Decimal:
To convert a fraction to a decimal, we divide the numerator by the denominator:
3 ÷ 700 ≈ 0.0042857
This decimal representation shows the value of 30/7000 as approximately 0.0042857. The "≈" symbol indicates that this is an approximation, as the decimal representation of this fraction is non-terminating (it continues infinitely).
3. Converting to a Percentage:
A percentage represents a fraction out of 100. To convert a decimal to a percentage, we multiply by 100 and add the "%" symbol:
0.0042857 × 100 ≈ 0.42857%
Therefore, 30/7000 is approximately 0.42857%. This percentage representation provides a readily understandable way to express the proportion of 30 out of 7000.
Understanding the Significance of Different Representations
The choice between representing a value as a fraction, decimal, or percentage depends on the context.
-
Fractions: Fractions are useful when precision is paramount and you want to maintain the exact value without rounding. They are ideal for representing precise proportions or parts of a whole.
-
Decimals: Decimals are helpful when dealing with calculations and comparisons, especially when using calculators or computers. They provide a direct numerical representation that's easy to interpret and manipulate.
-
Percentages: Percentages are excellent for communicating proportions to a broader audience. They are intuitive and easy to understand, making them suitable for conveying relative quantities in everyday contexts, such as sales discounts, interest rates, or statistical data.
Further Exploration: Proportions and Ratios
The problem "What is 30/7000?" is fundamentally a problem involving proportions and ratios. A ratio is a comparison between two quantities, while a proportion is a statement of equality between two ratios. We can express the relationship between 30 and 7000 as a ratio: 30:7000. This ratio can then be used to solve other related problems involving proportions.
For example, if we had a larger quantity of 70,000 items, we could use the proportion to find out how many would correspond to the same ratio:
30/7000 = x/70000
Solving for x, we get:
x = (30/7000) * 70000 = 300
This shows that if we have 70,000 items, 300 of them would represent the same proportion as 30 out of 7000.
Applications in Real-World Scenarios
Understanding fractions, decimals, and percentages, and their application in solving problems like "What is 30/7000?" has wide-ranging real-world applications:
- Finance: Calculating interest rates, determining loan repayments, analyzing investment returns.
- Science: Expressing experimental results, calculating concentrations, modeling physical phenomena.
- Engineering: Determining material ratios, calculating structural loads, designing systems.
- Statistics: Representing data, analyzing probabilities, conducting statistical tests.
- Business: Calculating profit margins, analyzing market share, managing budgets.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, absolutely! A calculator can efficiently convert fractions to decimals and percentages. Simply divide the numerator (30) by the denominator (7000).
Q: What if the numbers were larger or smaller?
A: The same principles apply. Always simplify the fraction first if possible, then convert it to a decimal or percentage using the methods described above.
Q: Why is the decimal approximation so long?
A: The decimal representation of 30/7000 is non-terminating because the simplified fraction, 3/700, has a denominator that is not a power of 10 (i.e., it is not 10, 100, 1000, etc.). Therefore, the decimal representation contains repeating or non-repeating digits that continue indefinitely.
Q: Are there other ways to express this proportion?
A: Yes, you can express this proportion in various ways, such as using ratios (30:7000), or by describing it verbally (30 out of 7000). The best representation depends on the context and the intended audience.
Conclusion: Mastering Fundamental Concepts
This article provided a comprehensive exploration of the seemingly simple question, "What is 30/7000?". We went beyond merely stating the answer, delving into the fundamental concepts of fractions, decimals, and percentages, demonstrating their interrelationship and explaining their applications in various real-world contexts. By understanding these concepts, you'll not only be able to solve similar mathematical problems but also gain valuable insights into proportional reasoning and its significance in various disciplines. Mastering these fundamental mathematical skills is essential for success in numerous academic and professional pursuits. The ability to confidently work with fractions, decimals, and percentages opens doors to more advanced mathematical concepts and problem-solving capabilities. Remember that practice is key; the more you work with these concepts, the more comfortable and proficient you'll become.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 30 Of 7000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.