What Is 25 Percent Of 150
sicesbrasil
Sep 23, 2025 · 5 min read
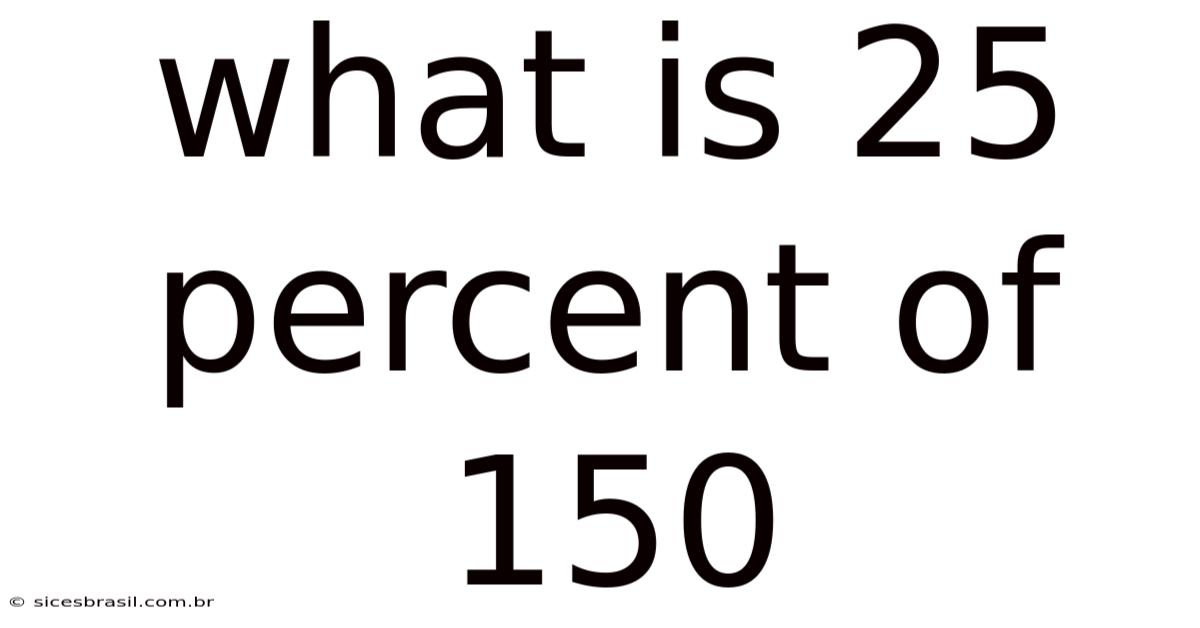
Table of Contents
What is 25 Percent of 150? A Comprehensive Guide to Percentages
Finding 25 percent of 150 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various aspects of life, from calculating discounts to understanding financial reports. This comprehensive guide will not only show you how to calculate 25% of 150 but also delve deeper into the concept of percentages, offering practical examples and different calculation methods. We'll explore the mathematical concepts involved, provide various approaches to solve the problem, and even touch upon real-world applications. By the end, you'll not only know the answer but also have a solid grasp of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" is derived from the Latin "per centum," meaning "out of one hundred." Therefore, 25% means 25 out of 100, which can also be represented as the fraction 25/100 or the decimal 0.25. Understanding this fundamental relationship is key to mastering percentage calculations.
Method 1: Using the Fraction Method
This method leverages the fractional representation of percentages. Since 25% is equivalent to 25/100, we can express the problem as:
(25/100) * 150
Simplifying the fraction, 25/100 reduces to 1/4. Therefore, the calculation becomes:
(1/4) * 150 = 150/4 = 37.5
Therefore, 25% of 150 is 37.5.
Method 2: Using Decimal Conversion
This method utilizes the decimal equivalent of a percentage. As mentioned earlier, 25% is equal to 0.25. Therefore, the calculation is:
0.25 * 150 = 37.5
This method is often preferred for its simplicity and ease of use with calculators. Again, we arrive at the answer: 37.5.
Method 3: Using Proportions
This method involves setting up a proportion to solve for the unknown value. We can express the problem as:
x/150 = 25/100
To solve for x, we can cross-multiply:
100x = 25 * 150
100x = 3750
x = 3750/100
x = 37.5
Once more, we find that 25% of 150 is 37.5.
Method 4: Breaking it Down
This method simplifies the calculation by breaking down the percentage into smaller, easier-to-handle parts. We know that 10% of 150 is 15 (150/10 = 15). Since 25% is 2.5 times 10% (25/10 = 2.5), we can calculate:
15 * 2.5 = 37.5
This method is particularly useful for mental calculations or when dealing with percentages that aren't easily converted to simple fractions.
Real-World Applications of Percentage Calculations
Understanding percentages is vital in various real-world scenarios:
- Sales and Discounts: Calculating discounts on sale items. For example, a 25% discount on a $150 item equates to a $37.50 saving.
- Taxes: Determining the amount of sales tax or income tax owed.
- Finance: Calculating interest earned on savings accounts or interest paid on loans.
- Statistics: Interpreting statistical data presented as percentages, like survey results or market share.
- Tipping: Calculating appropriate tips in restaurants or for service providers.
- Grades and Scores: Understanding test scores and academic performance presented as percentages.
- Profit Margins: Determining the profitability of a business by calculating the profit margin as a percentage of revenue.
Beyond the Basics: Working with Different Percentages
While we focused on 25%, the same principles apply to calculating other percentages. Let's consider a few examples:
- Finding 15% of 150: This can be calculated as 0.15 * 150 = 22.5
- Finding 75% of 150: This can be calculated as 0.75 * 150 = 112.5
- Finding 1% of 150: This is simply 150/100 = 1.5. This is useful as a building block for other percentages.
Understanding Percentage Increase and Decrease
Percentages are also used to express changes in values. For example, if a value increases from 100 to 125, the percentage increase is calculated as:
[(125 - 100) / 100] * 100% = 25%
Similarly, if a value decreases from 150 to 112.5, the percentage decrease is:
[(150 - 112.5) / 150] * 100% = 25%
In both cases, the change represents a 25% change in the original value.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method depends on your preference and the specific percentage. Using the decimal conversion (e.g., 25% = 0.25) is generally the most straightforward for most calculations, especially when using a calculator.
Q: How can I calculate percentages without a calculator?
A: For simpler percentages like 10%, 25%, 50%, or multiples thereof, mental math techniques are often sufficient. Breaking down the percentage into smaller, manageable parts (as shown in Method 4) can also be helpful.
Q: What if the percentage is not a whole number (e.g., 25.5%)?
A: The same principles apply. Convert the percentage to its decimal equivalent (25.5% = 0.255) and multiply it by the number.
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, numerous online percentage calculators are readily available. Simply search for "percentage calculator" on your preferred search engine.
Q: Why is understanding percentages important?
A: Understanding percentages is a fundamental skill applicable in various areas of life, including finance, shopping, education, and data analysis. It empowers you to make informed decisions and understand information presented numerically.
Conclusion
Calculating 25% of 150, as we've shown, yields the answer 37.5. However, the true value of this exercise lies not just in obtaining the answer but in understanding the broader concept of percentages and their application in diverse contexts. Mastering percentage calculations equips you with a valuable skill that will serve you well in both academic and professional settings. Remember the different methods—using fractions, decimals, proportions, or breaking down the calculation—and choose the method that best suits your needs and the complexity of the problem. The more you practice, the more comfortable and proficient you will become with percentage calculations.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.