What Is 25 Of 75
sicesbrasil
Sep 23, 2025 · 5 min read
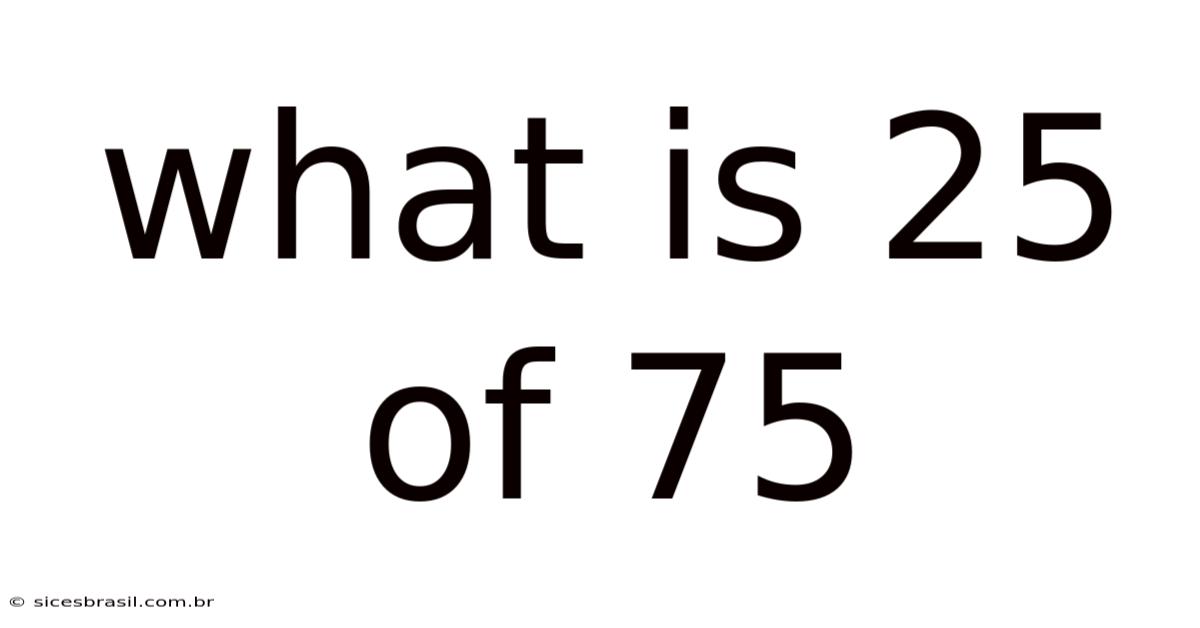
Table of Contents
What is 25% of 75? A Comprehensive Guide to Percentages and Their Applications
Finding 25% of 75 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept in mathematics: percentages. This seemingly basic calculation is crucial in various fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will not only show you how to calculate 25% of 75 but also explore the underlying principles of percentages, offer multiple solution methods, and delve into real-world applications to solidify your understanding.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent" or "out of one hundred." For example, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25. Understanding this fundamental equivalence is key to working with percentages effectively.
Calculating 25% of 75: Three Methods
There are several ways to calculate 25% of 75. Let's explore three common methods:
Method 1: Using the Fraction Equivalent
As mentioned earlier, 25% is equivalent to the fraction 25/100. We can express "25% of 75" as a mathematical equation:
(25/100) * 75
Simplifying the fraction, we get:
(1/4) * 75
This simplifies the calculation to:
75 / 4 = 18.75
Therefore, 25% of 75 is 18.75.
Method 2: Using Decimal Equivalents
We can also convert 25% to its decimal equivalent, 0.25. The calculation then becomes:
0.25 * 75 = 18.75
This method is often quicker and easier for those comfortable with decimal multiplication. Again, the answer is 18.75.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between percentages and their corresponding values. We can set up a proportion:
25/100 = x/75
Here, 'x' represents the unknown value (25% of 75). To solve for 'x', we cross-multiply:
25 * 75 = 100 * x
1875 = 100x
x = 1875 / 100
x = 18.75
Once again, the result is 18.75.
Beyond the Calculation: Real-World Applications of Percentages
Understanding how to calculate percentages isn't just about solving math problems; it's a vital skill for navigating everyday life and professional settings. Here are some examples:
-
Shopping and Sales: Calculating discounts is a common application. If a store offers a 25% discount on an item priced at $75, you'll save $18.75 (as we've just calculated). This allows you to determine the final price quickly.
-
Finance and Budgeting: Percentages are essential for understanding interest rates, taxes, and investment returns. For instance, calculating the interest earned on a savings account or determining the amount of tax payable on income involves percentage calculations.
-
Data Analysis and Statistics: Percentages are widely used to represent data proportions and trends in various fields like market research, demographics, and scientific studies. For example, analyzing survey results often involves expressing responses as percentages of the total sample size.
-
Science and Engineering: Percentages play a crucial role in expressing concentrations, efficiencies, and error margins in scientific experiments and engineering projects. For instance, the percentage purity of a chemical compound or the efficiency of a machine is frequently expressed as a percentage.
-
Healthcare: Percentages are essential in healthcare for expressing medication dosages, blood composition, and various health metrics. Understanding these percentages is crucial for accurate diagnoses and treatment plans.
Expanding Your Understanding: Working with Different Percentages
While we've focused on 25%, the principles remain the same for other percentages. Here's how to approach calculations with different percentage values:
-
Calculating 10%: Finding 10% of a number is straightforward. Simply divide the number by 10. For example, 10% of 75 is 75/10 = 7.5
-
Calculating 5%: 5% is half of 10%. So, to find 5% of a number, find 10% and then divide the result by 2. 5% of 75 is (75/10)/2 = 3.75.
-
Calculating other percentages: For any other percentage, convert it to a fraction or decimal and multiply it by the number. For instance, to find 30% of 75, calculate (30/100) * 75 = 22.5 or 0.30 * 75 = 22.5
Frequently Asked Questions (FAQ)
Q1: What if I need to find more than 100% of a number?
A: Finding more than 100% of a number simply means finding a value greater than the original number. For example, 150% of 75 is (150/100) * 75 = 112.5.
Q2: Can I use a calculator for percentage calculations?
A: Yes, absolutely! Calculators are extremely helpful for quick and accurate percentage calculations, particularly with more complex scenarios. Most calculators have a percentage function (%) button that simplifies the process.
Q3: Are there any online tools or websites for percentage calculations?
A: Yes, many online calculators and converters are readily available. These tools can be helpful for verifying your calculations or for tackling more complex percentage problems.
Q4: How do I calculate the percentage increase or decrease between two numbers?
A: To calculate a percentage increase or decrease, follow these steps:
- Find the difference between the two numbers.
- Divide the difference by the original number.
- Multiply the result by 100 to express it as a percentage.
For example, if a number increases from 50 to 75, the percentage increase is:
(75 - 50) / 50 * 100 = 50%
Q5: What are some common errors to avoid when calculating percentages?
A: Common errors include:
- Incorrect decimal placement: Ensure you correctly convert percentages to decimals before multiplying.
- Misinterpreting the problem: Carefully read the problem to understand exactly what percentage you need to calculate.
- Rounding errors: Be mindful of rounding errors, especially when working with multiple steps.
Conclusion
Calculating 25% of 75, which equals 18.75, might seem trivial at first glance. However, understanding the underlying principles of percentages and the various methods for calculation provides a foundation for tackling more complex mathematical problems and real-world scenarios. This skill is indispensable in various aspects of life, from personal finance to professional endeavors, highlighting the practical significance of mastering this seemingly simple concept. By understanding the different methods and applications explored in this guide, you'll be well-equipped to confidently handle percentages in any context. Remember to practice regularly and utilize the various techniques discussed to solidify your understanding and enhance your problem-solving skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 25 Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.