What Is 10 Of 250
sicesbrasil
Sep 23, 2025 · 6 min read
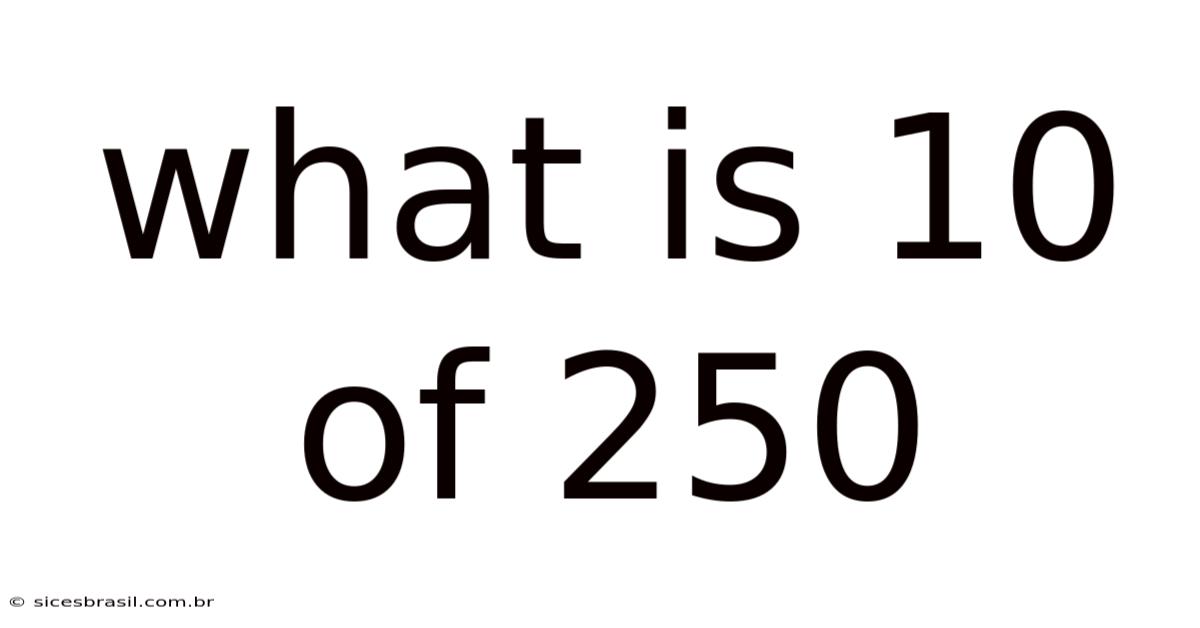
Table of Contents
What is 10% of 250? A Deep Dive into Percentages and Their Applications
Finding 10% of 250 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to calculate percentages, especially this seemingly basic example, unlocks a powerful tool with far-reaching applications in numerous fields, from everyday budgeting to complex financial modeling. This article will not only show you how to calculate 10% of 250, but also explore the underlying principles of percentage calculations, different methods to arrive at the answer, and delve into real-world examples demonstrating the practical significance of percentage calculations.
Understanding Percentages: The Foundation
Before we tackle the specific problem of finding 10% of 250, let's solidify our understanding of percentages. A percentage is simply a fraction where the denominator is always 100. The "%" symbol represents "per cent," meaning "out of one hundred." So, 10% can be written as 10/100, or its simplified fraction, 1/10.
This understanding is crucial. Percentages provide a standardized way to compare proportions. Whether we're discussing sales discounts, exam scores, or population growth rates, percentages offer a clear and easily understandable representation of relative amounts.
Method 1: Direct Calculation using Decimal Conversion
The most straightforward method for calculating 10% of 250 involves converting the percentage to a decimal. Since 10% is equivalent to 10/100, we can simplify this to 0.1. To find 10% of 250, we simply multiply 250 by 0.1:
250 * 0.1 = 25
Therefore, 10% of 250 is 25.
Method 2: Fractional Approach
Alternatively, we can approach this problem using the fractional representation of 10%, which is 1/10. Finding 10% of 250 is equivalent to finding one-tenth of 250. This can be calculated as:
250 * (1/10) = 250/10 = 25
Again, the result is 25. This method highlights the direct relationship between fractions and percentages.
Method 3: Proportion Method (for more complex scenarios)
While the previous methods are efficient for simple percentage calculations, the proportion method is particularly useful when dealing with more complex problems where you might need to find an unknown percentage of a known value, or vice versa. Let's illustrate this with our example:
We can set up a proportion:
10/100 = x/250
Where 'x' represents the unknown value (10% of 250). To solve for x, we cross-multiply:
10 * 250 = 100 * x
2500 = 100x
x = 2500/100 = 25
This method reaffirms that 10% of 250 is 25. The beauty of this method lies in its adaptability to various percentage problems, allowing you to solve for any unknown variable.
Real-World Applications: Beyond the Classroom
The seemingly simple calculation of 10% of 250 has a vast range of practical applications across various domains:
-
Sales and Discounts: Imagine a store offering a 10% discount on a $250 item. The discount amount would be $25, resulting in a final price of $225. This is a common scenario in retail and e-commerce.
-
Taxes and Tipping: Calculating sales tax or a tip often involves percentages. If the sales tax is 10% on a $250 purchase, the tax amount would be $25. Similarly, a 10% tip on a $250 restaurant bill would also be $25.
-
Financial Investments: Understanding percentages is fundamental in finance. Calculating interest earned on investments, analyzing stock market returns, or understanding loan interest rates all rely on percentage calculations. For example, a 10% return on a $250 investment would yield $25 in profit.
-
Data Analysis and Statistics: Percentages are used extensively in data analysis to represent proportions, trends, and comparisons. In scientific research, survey analysis, and market research, percentages are integral to interpreting data and drawing meaningful conclusions. For instance, if 10% of a survey sample of 250 people responded positively to a question, it would represent 25 positive responses.
-
Scientific Measurements and Conversions: In some scientific fields, data representation might involve percentage changes or ratios, building upon fundamental percentage understanding.
-
Everyday Budgeting: Tracking expenses and savings often involves calculating percentages of income. For example, someone might budget 10% of their income ($250) for savings, allocating $25 towards their savings goal.
Expanding Your Understanding: Beyond 10% of 250
While this article focused on calculating 10% of 250, the principles discussed apply to a wide range of percentage problems. You can adapt these methods to calculate any percentage of any number. For instance:
-
Calculating 25% of 250: Convert 25% to a decimal (0.25) and multiply by 250: 0.25 * 250 = 62.5
-
Calculating X% of Y: The proportion method is particularly useful here. You would set up the proportion: X/100 = Z/Y, where Z is the unknown value.
-
Finding what percentage one number is of another: For example, finding what percentage 25 is of 250, you would set up the proportion: X/100 = 25/250, and solve for X.
Mastering percentage calculations is a valuable life skill. It empowers you to confidently tackle various real-world problems, analyze data, make informed financial decisions, and understand quantitative information presented in various contexts.
Frequently Asked Questions (FAQs)
Q1: What is the easiest way to calculate percentages?
A1: The easiest method is often converting the percentage to a decimal and multiplying it by the number. For example, 15% of 300 is calculated as 0.15 * 300 = 45.
Q2: How can I calculate percentages without a calculator?
A2: For simpler percentages (like 10%, 25%, 50%), you can use fractional equivalents. For more complex percentages, you can use the proportion method and perform the necessary multiplication and division.
Q3: Are there any online tools to calculate percentages?
A3: Yes, numerous online percentage calculators are available which can help you quickly and accurately calculate various percentage-related problems.
Q4: Why are percentages important?
A4: Percentages provide a standardized way to compare proportions, making it easier to understand and analyze data across various contexts, from finance to science to everyday life. They help in understanding relative amounts and making informed decisions.
Q5: What are some common mistakes to avoid when calculating percentages?
A5: Common mistakes include incorrectly converting percentages to decimals, using the wrong formula, and misinterpreting the problem statement. Always double-check your work and ensure you understand what the question is asking.
Conclusion
In conclusion, while finding 10% of 250 yields a simple answer (25), the underlying concept of percentage calculation has significant implications across various fields. This article has explored multiple methods for calculating percentages, highlighting their versatility and practical utility. Understanding percentages is not just about solving mathematical problems; it's about gaining a powerful tool for interpreting data, making informed decisions, and navigating the quantitative aspects of everyday life and professional endeavors. Mastering this seemingly simple concept opens doors to a deeper understanding of the world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is 10 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.