Solve 4x 2 25 0
sicesbrasil
Sep 24, 2025 · 5 min read
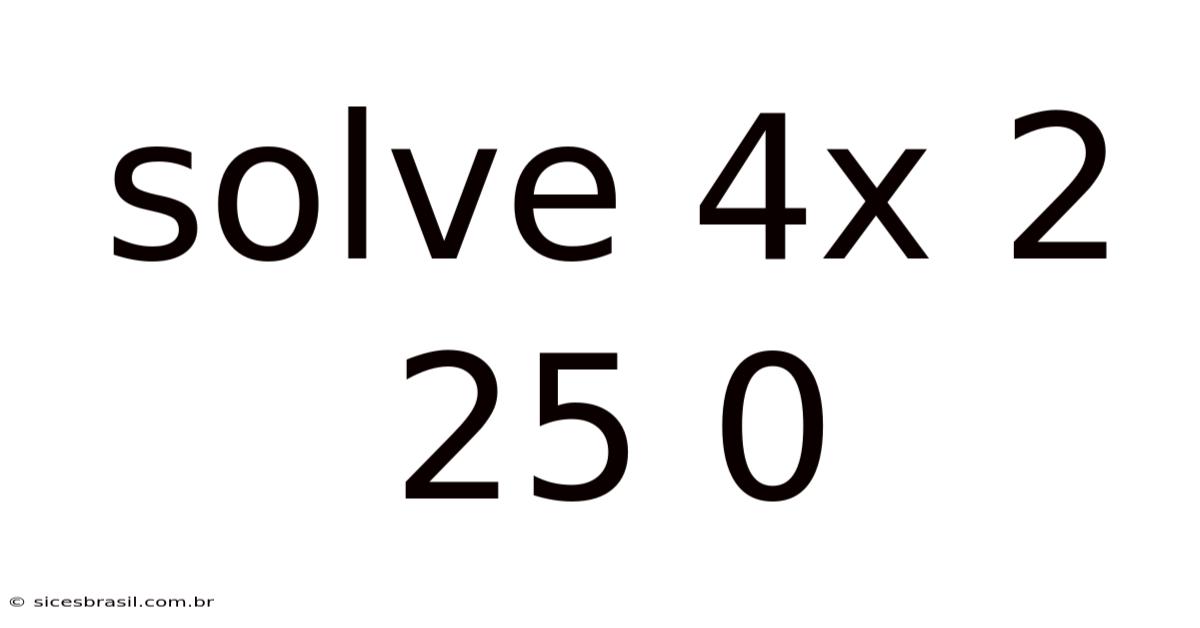
Table of Contents
Solving the Quadratic Equation: 4x² + 25 = 0
This article will comprehensively guide you through solving the quadratic equation 4x² + 25 = 0. We'll explore various methods, delve into the underlying mathematical concepts, and address frequently asked questions. Understanding how to solve this type of equation is crucial for various applications in mathematics, physics, and engineering. This seemingly simple equation offers a great opportunity to understand the nature of quadratic equations and their solutions, including real and complex numbers.
Introduction to Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually x) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a is not equal to zero. Our specific equation, 4x² + 25 = 0, is a special case where b = 0. This simplification allows us to use specific techniques to find the solutions efficiently.
Method 1: Solving by Isolating x²
Since our equation lacks a linear term (bx), the most straightforward approach is to isolate x² and then solve for x. Let's break down the steps:
-
Subtract 25 from both sides: This step aims to isolate the term containing x². The equation becomes: 4x² = -25
-
Divide both sides by 4: This isolates x². The equation simplifies to: x² = -25/4
-
Take the square root of both sides: Remember that the square root of a number has two solutions – a positive and a negative root. Therefore, we have: x = ±√(-25/4)
-
Simplify the square root: We encounter a negative number under the square root. This introduces imaginary numbers. The square root of -1 is defined as the imaginary unit i. We can rewrite the equation as: x = ±(√25/√4) * i = ±(5/2)i
Therefore, the solutions to the equation 4x² + 25 = 0 are x = (5/2)i and x = -(5/2)i. These are complex conjugate solutions.
Method 2: Using the Quadratic Formula
The quadratic formula provides a general solution for any quadratic equation of the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
In our case, a = 4, b = 0, and c = 25. Substituting these values into the quadratic formula:
x = [-0 ± √(0² - 4 * 4 * 25)] / (2 * 4)
x = ± √(-400) / 8
x = ± √(-1 * 400) / 8
x = ± (20i) / 8
x = ± (5/2)i
This confirms our previous result: x = (5/2)i and x = -(5/2)i. The quadratic formula provides a robust method applicable to all quadratic equations, even those with complex solutions.
Understanding Complex Numbers
The solutions to our equation involve complex numbers. A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is the imaginary unit (√-1). In our case, a = 0 and b = ±5/2. Complex numbers extend the real number system and are essential for various mathematical and scientific applications. The solutions (5/2)i and -(5/2)i are called complex conjugates; they have the same real part (0) and opposite imaginary parts.
Graphical Representation of the Solutions
While we can't directly plot complex numbers on a traditional number line (which represents real numbers), we can visualize them on a complex plane. The complex plane has a horizontal axis representing the real part and a vertical axis representing the imaginary part. Our solutions, (5/2)i and -(5/2)i, would be plotted on the imaginary axis, one at 2.5 units above the origin and the other at 2.5 units below the origin.
The Discriminant and Nature of Roots
The expression b² - 4ac within the quadratic formula is called the discriminant. It determines the nature of the roots (solutions) of the quadratic equation:
- b² - 4ac > 0: Two distinct real roots.
- b² - 4ac = 0: One real root (a repeated root).
- b² - 4ac < 0: Two complex conjugate roots.
In our equation, b² - 4ac = 0² - 4 * 4 * 25 = -400, which is less than 0. This confirms that the equation has two complex conjugate roots, as we found.
Applications of Quadratic Equations with Complex Roots
While it might seem that complex roots are less practical than real roots, they have significant applications in various fields:
- Electrical Engineering: Complex numbers are extensively used in AC circuit analysis to represent impedance, voltage, and current.
- Quantum Mechanics: Complex numbers are fundamental to the mathematical framework of quantum mechanics.
- Signal Processing: Complex numbers are used to represent signals and their frequencies in signal processing.
- Fluid Dynamics: Complex analysis helps solve certain fluid flow problems.
Frequently Asked Questions (FAQ)
Q1: Why do we get imaginary numbers as solutions?
A1: We obtain imaginary numbers because the discriminant (b² - 4ac) is negative. Taking the square root of a negative number necessitates the use of the imaginary unit i.
Q2: Are complex conjugate solutions always paired together?
A2: Yes, for quadratic equations with real coefficients (like our example), complex roots always appear as conjugate pairs.
Q3: Can I solve this equation using factoring?
A3: While factoring is a common method for solving quadratic equations, it's less straightforward in this case because the equation doesn't easily factor over the real numbers. Factoring can still be done using complex numbers but is less efficient than the methods described above.
Q4: What does it mean geometrically that the solutions are purely imaginary?
A4: Geometrically, the purely imaginary solutions indicate that the parabola represented by the equation 4x² + 25 = 0 does not intersect the real x-axis. The parabola is entirely above the x-axis.
Q5: Are there other types of equations that can yield complex solutions?
A5: Yes, many higher-order polynomial equations and even transcendental equations can produce complex solutions. The presence of a negative quantity under a square root (or other even root) is a common indicator.
Conclusion
Solving the quadratic equation 4x² + 25 = 0 demonstrates the importance of understanding complex numbers and their applications. While the equation appears simple at first glance, it opens a door to deeper concepts in algebra and their relevance in various scientific and engineering disciplines. Both the isolation method and the quadratic formula are effective approaches, and choosing the most suitable method often depends on the specific form of the equation. The concepts explored here – complex numbers, the discriminant, and the graphical representation of complex roots – provide a solid foundation for further explorations in mathematics and its practical applications. Remember, the seemingly simple can often lead to surprisingly rich and rewarding mathematical insights.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve 4x 2 25 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.