4 9 As A Decimal
sicesbrasil
Sep 22, 2025 · 5 min read
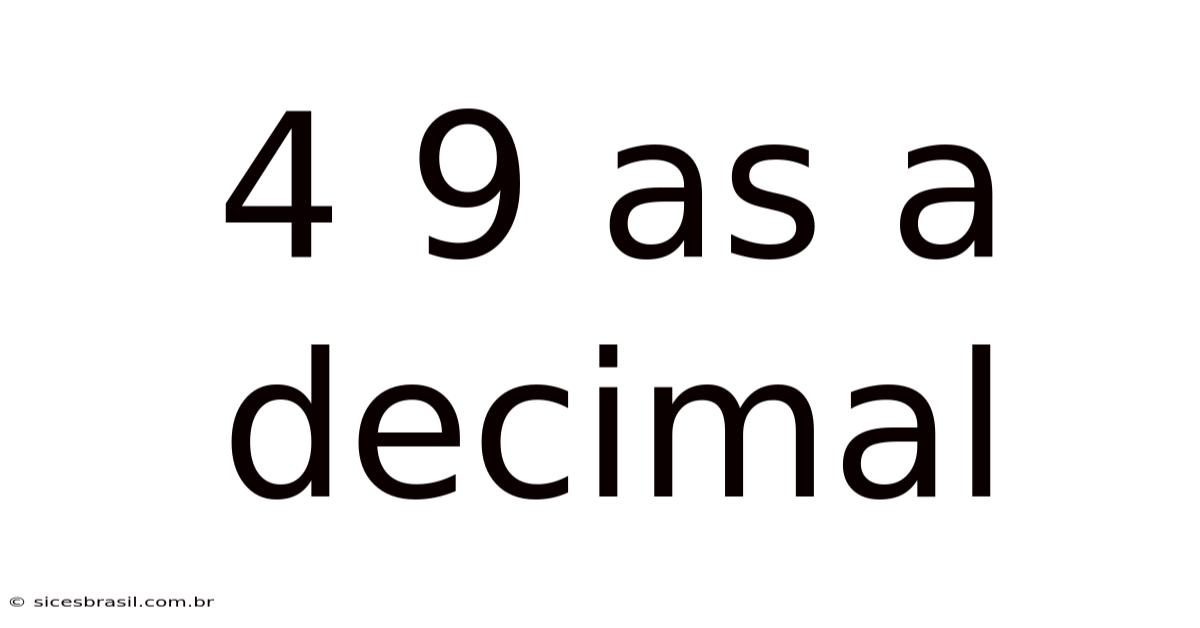
Table of Contents
Decoding 4/9: A Deep Dive into Decimal Conversions and Beyond
Understanding fractions and their decimal equivalents is fundamental to mathematics. This comprehensive guide explores the conversion of the fraction 4/9 into its decimal form, delving into the underlying principles, exploring related concepts, and answering frequently asked questions. We'll move beyond a simple answer and equip you with a robust understanding of this seemingly simple conversion.
Understanding Fractions and Decimals
Before we dive into the specifics of 4/9, let's establish a foundational understanding of fractions and decimals. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
A decimal, on the other hand, represents a part of a whole using a base-10 system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. Decimals are a convenient way to express fractions, especially when performing calculations.
Converting 4/9 to a Decimal: The Long Division Method
The most straightforward method for converting a fraction to a decimal is through long division. We divide the numerator (4) by the denominator (9):
0.4444...
9 | 4.0000
-3.6
0.40
-0.36
0.040
-0.036
0.0040
-0.0036
0.0004...
As you can see, the division process continues indefinitely. We obtain a repeating decimal, specifically 0.4444... This is often represented as 0.4̅, where the bar above the 4 indicates that the digit repeats infinitely.
Understanding Repeating Decimals
The result of converting 4/9 to a decimal reveals a key characteristic: it's a repeating decimal. Not all fractions result in repeating decimals. Some fractions convert to terminating decimals, meaning the division process ends after a finite number of steps. The difference lies in the prime factorization of the denominator.
-
Terminating Decimals: Fractions whose denominators, when simplified to their lowest terms, have only 2 and/or 5 as prime factors will result in terminating decimals. For example, 1/2 = 0.5, 1/4 = 0.25, and 1/5 = 0.2.
-
Repeating Decimals: Fractions whose denominators, when simplified, contain prime factors other than 2 and 5 will result in repeating decimals. This is the case with 4/9, where the denominator (9) has a prime factorization of 3 x 3. Therefore, it produces a repeating decimal.
The Concept of Rational Numbers
Both fractions and terminating/repeating decimals represent rational numbers. A rational number is any number that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. Essentially, all fractions are rational numbers, and all rational numbers can be expressed as either terminating or repeating decimals.
Alternative Methods for Conversion
While long division is a direct and understandable approach, other methods can be used to convert fractions to decimals. These methods are particularly useful for more complex fractions.
-
Using a Calculator: The simplest approach for most practical purposes is using a calculator. Simply input 4 ÷ 9 and the calculator will display the decimal equivalent, likely showing 0.444444... or a rounded version like 0.444.
-
Conversion to an Equivalent Fraction: Sometimes, converting the fraction to an equivalent fraction with a denominator that is a power of 10 can simplify the conversion to a decimal. However, this isn't always feasible, especially with fractions like 4/9.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals has numerous practical applications across various fields:
-
Finance: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals.
-
Engineering: Precise measurements and calculations in engineering frequently require converting fractions to decimals for accurate results.
-
Science: Many scientific measurements and calculations rely on decimals for greater precision.
-
Everyday Life: From splitting bills equally to understanding sale prices, the ability to convert fractions to decimals is valuable in everyday situations.
Beyond the Basics: Exploring Related Concepts
Understanding 4/9 as a decimal opens doors to exploring several related mathematical concepts:
-
Infinite Series: The repeating decimal 0.4̅ can be represented as an infinite geometric series: 4/10 + 4/100 + 4/1000 + ... This series converges to the value 4/9.
-
Continued Fractions: Rational numbers can also be represented as continued fractions. While beyond the scope of this introduction, exploring continued fractions provides a deeper understanding of the relationship between fractions and decimals.
-
Approximations: In practical applications, we often use approximations of repeating decimals. For example, instead of 0.4̅, we might use 0.44 or 0.444 depending on the required level of accuracy.
Frequently Asked Questions (FAQ)
Q: Is 0.4̅ exactly equal to 4/9?
A: Yes, 0.4̅ is exactly equal to 4/9. The bar above the 4 signifies that the digit 4 repeats infinitely.
Q: Why does 4/9 result in a repeating decimal?
A: Because the denominator 9 (when simplified) has prime factors other than 2 and 5.
Q: How can I convert other fractions to decimals?
A: Use the long division method or a calculator. Consider converting to an equivalent fraction with a power-of-10 denominator if possible.
Q: Are there any fractions that don't result in either a terminating or repeating decimal?
A: No. All fractions represent rational numbers, which can always be expressed as either a terminating or repeating decimal. Numbers that cannot be expressed as fractions are called irrational numbers (e.g., π and √2).
Conclusion: Mastering Decimal Conversions
Converting 4/9 to its decimal equivalent, 0.4̅, is more than just a simple mathematical operation. It's a gateway to understanding fundamental concepts like rational numbers, repeating decimals, and the relationships between fractions and decimals. By grasping these concepts, you'll not only be able to perform the conversion accurately but also appreciate the underlying mathematical principles at play. The ability to comfortably work with fractions and decimals is crucial for success in various academic and professional fields. Continue to practice these conversions, and you'll build a strong foundation in mathematical literacy.
Latest Posts
Related Post
Thank you for visiting our website which covers about 4 9 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.