3 X 2 4 X 2
sicesbrasil
Sep 23, 2025 · 6 min read
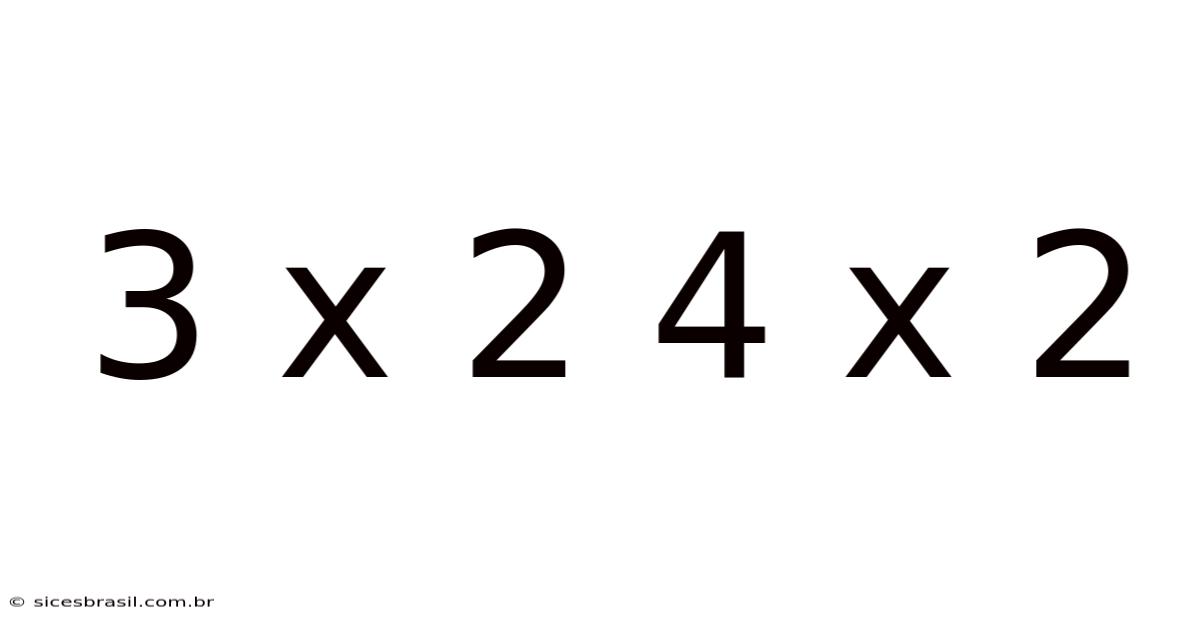
Table of Contents
Decoding 3 x 2, 4 x 2: Exploring Multiplication, Area, and Volume in Multiple Dimensions
This article delves into the seemingly simple mathematical expressions "3 x 2" and "4 x 2," revealing their multifaceted applications beyond basic arithmetic. We'll explore their significance in understanding fundamental concepts like multiplication, area calculation in two dimensions, and even extending the concept to visualize volume in three dimensions. Understanding these foundational elements is crucial for grasping more advanced mathematical concepts in geometry, algebra, and beyond.
Understanding the Fundamentals of Multiplication
At its core, "3 x 2" and "4 x 2" represent multiplication problems. Multiplication is a fundamental arithmetic operation that essentially involves repeated addition. In the case of "3 x 2," it signifies adding the number 2 three times: 2 + 2 + 2 = 6. Similarly, "4 x 2" means adding the number 2 four times: 2 + 2 + 2 + 2 = 8. This simple concept forms the basis for understanding more complex mathematical operations.
Key takeaway: Multiplication provides a concise way to represent repeated addition, streamlining calculations and simplifying complex problems.
Visualizing 3 x 2 and 4 x 2: Area in Two Dimensions
Beyond simple addition, these expressions can be vividly visualized as areas. Imagine a rectangle. "3 x 2" can represent a rectangle with a length of 3 units and a width of 2 units. The area of this rectangle is calculated by multiplying its length and width: 3 units x 2 units = 6 square units. This means the rectangle can be filled with 6 unit squares.
Similarly, "4 x 2" represents a rectangle with a length of 4 units and a width of 2 units. Its area is calculated as 4 units x 2 units = 8 square units. This visual representation helps solidify the concept of multiplication and its relationship to geometric shapes.
Key takeaway: Multiplication is directly applicable to calculating the area of rectangular shapes. The numbers represent the dimensions, and the product represents the area.
Extending the Concept: Volume in Three Dimensions
While "3 x 2" and "4 x 2" primarily relate to two-dimensional areas, we can extend this concept to three dimensions to understand volume. Imagine a rectangular prism (a box). To calculate its volume, we need three dimensions: length, width, and height.
Let's consider a rectangular prism with a base represented by "3 x 2" (length 3, width 2). If we give this prism a height of, say, 1 unit, its volume would be 3 units x 2 units x 1 unit = 6 cubic units. This means the prism can be filled with 6 unit cubes.
Now, let's consider another rectangular prism with a base of "4 x 2" (length 4, width 2) and a height of 2 units. Its volume would be 4 units x 2 units x 2 units = 16 cubic units. Visualizing these prisms helps to connect the multiplication concept to three-dimensional space.
Key takeaway: Extending the multiplication concept to three dimensions allows for the calculation of volume in rectangular prisms. Each number represents a dimension, and their product represents the volume.
Real-World Applications: Beyond the Classroom
The seemingly simple expressions "3 x 2" and "4 x 2" have far-reaching practical applications in various fields:
-
Construction and Engineering: Calculating the area of walls, floors, and roofs, and the volume of materials like concrete and soil are fundamental tasks in construction and engineering, directly relying on multiplication.
-
Interior Design and Decoration: Determining the amount of paint, tiles, or carpet needed for a room involves calculating areas, using multiplication.
-
Packaging and Shipping: Calculating the volume of boxes to optimize shipping space and minimize costs is crucial in logistics and supply chain management.
-
Gardening and Farming: Determining the area of a garden plot to plan planting and calculate fertilizer needs directly utilizes multiplication.
-
Cooking and Baking: Scaling recipes often requires multiplication to adjust ingredient quantities proportionally.
Beyond Rectangles: Exploring Other Shapes
While we've focused on rectangles and rectangular prisms, the principles of multiplication extend to other shapes. For example, calculating the area of a triangle involves multiplying the base and height and then dividing by two (Area = 1/2 * base * height). Even for more complex shapes, the underlying principle of multiplication remains central to area and volume calculations, often utilizing calculus in more advanced cases.
Exploring Different Number Systems
While we've used base-10 (decimal) numbers, the principles of multiplication apply equally to other number systems, such as binary (base-2) which is fundamental in computer science. In binary, "10" (which is 2 in decimal) multiplied by "11" (which is 3 in decimal) would still result in "110" (which is 6 in decimal). The fundamental concept of repeated addition remains consistent.
Addressing Common Misconceptions
A common misconception is that multiplication is solely about speed. While it certainly streamlines calculations, its true power lies in its ability to represent relationships between quantities and dimensions, which has profound applications beyond simple arithmetic.
Another misconception relates to the commutative property of multiplication – that the order of the numbers doesn't matter (3 x 2 = 2 x 3). While true for the final numerical result, the physical representation can differ. A rectangle with length 3 and width 2 is not identical to a rectangle with length 2 and width 3, although their areas are the same. This subtle difference underscores the importance of understanding the underlying concepts.
Frequently Asked Questions (FAQs)
-
Q: What is the difference between 3 x 2 and 2 x 3? A: While the numerical result is the same (6), the visual representation as a rectangle differs. One has a length of 3 and width of 2, the other vice versa.
-
Q: Can multiplication be used for shapes other than rectangles? A: Yes, absolutely. It's a fundamental principle in calculating areas and volumes of various shapes, often requiring more complex formulas.
-
Q: How does multiplication relate to other mathematical operations? A: Multiplication is closely linked to addition (repeated addition), division (the inverse of multiplication), and exponents (repeated multiplication).
-
Q: Is multiplication only relevant to mathematics? A: No. It's a fundamental concept with widespread applications in science, engineering, finance, and many other fields.
-
Q: How can I improve my understanding of multiplication? A: Practice regularly, use visual aids like diagrams and models, and explore its applications in real-world contexts.
Conclusion: The Enduring Power of Simple Multiplication
The seemingly simple expressions "3 x 2" and "4 x 2" reveal the depth and versatility of the multiplication operation. From basic arithmetic to calculating areas and volumes, and from two-dimensional geometry to three-dimensional space, the principles of multiplication form a bedrock for understanding more complex mathematical concepts and solving real-world problems. By appreciating the foundational nature of these expressions, we unlock a deeper understanding of mathematics and its pervasive influence on our world. Further exploration of these concepts will invariably lead to a more robust mathematical foundation and a greater capacity for problem-solving across diverse fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about 3 X 2 4 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.