24 Is 80 Of What Number
sicesbrasil
Sep 24, 2025 · 5 min read
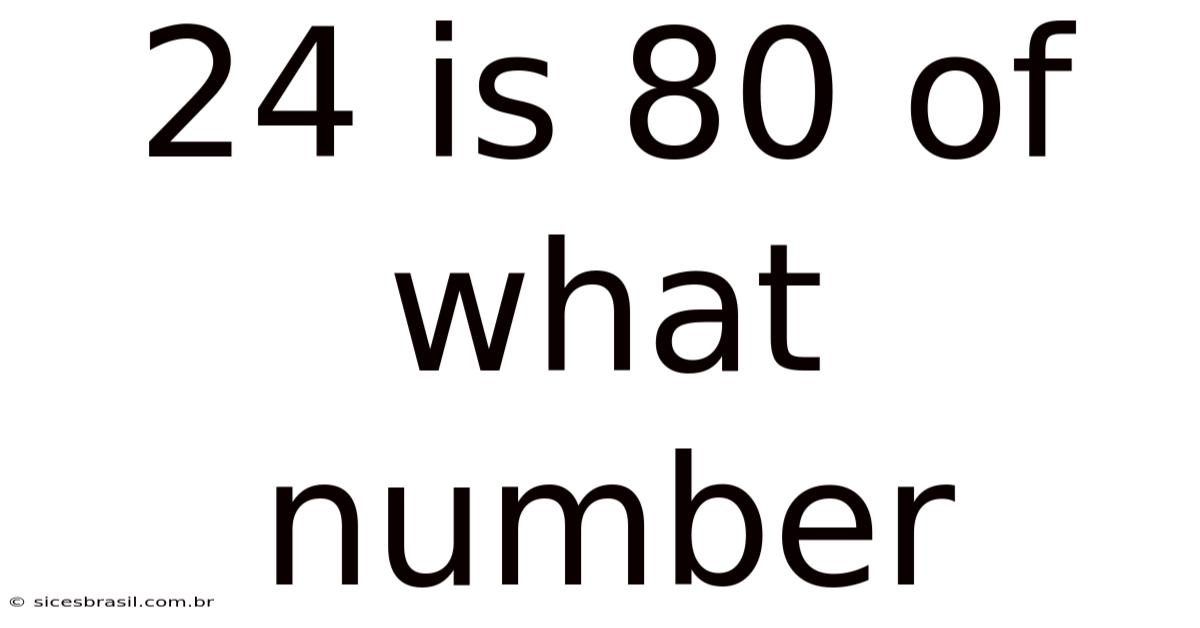
Table of Contents
24 is 80% of What Number? A Comprehensive Guide to Percentage Calculations
Finding out what number 24 represents 80% of is a common problem in mathematics, appearing frequently in various fields, from everyday finances to advanced statistical analysis. This article will not only provide the solution but also delve deep into the underlying concepts, exploring different methods to solve similar percentage problems and equipping you with the knowledge to tackle them confidently. We’ll cover various approaches, from simple arithmetic to algebraic solutions, ensuring a thorough understanding for learners of all levels.
Understanding Percentages
Before we dive into solving the problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100". For example, 80% can be written as 80/100 or its simplified fraction, 4/5. This means that 80% represents 80 parts out of a total of 100 equal parts.
Method 1: Using the Proportion Method
This is arguably the most intuitive method for solving percentage problems. We set up a proportion:
- Part/Whole = Percentage/100
In our problem, we know the part (24) and the percentage (80%). We need to find the whole number. Let's represent the unknown whole number with the variable 'x'. This gives us the proportion:
24/x = 80/100
To solve this, we can cross-multiply:
24 * 100 = 80 * x
2400 = 80x
Now, we isolate 'x' by dividing both sides of the equation by 80:
x = 2400 / 80
x = 30
Therefore, 24 is 80% of 30.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then setting up an equation. To convert a percentage to a decimal, we divide the percentage by 100. For 80%, this is 80/100 = 0.8.
We can then express the problem as an equation:
0.8 * x = 24
To solve for x, we divide both sides by 0.8:
x = 24 / 0.8
x = 30
Again, we find that 24 is 80% of 30.
Method 3: Using the Formula
A more direct formula can be derived from the proportion method. If we want to find the whole number (let's call it 'W') when we know the part (P) and the percentage (%), the formula is:
W = (P / %) * 100
Plugging in our values:
W = (24 / 80) * 100
W = 0.3 * 100
W = 30
This formula provides a quick and efficient way to solve these types of percentage problems.
Method 4: Algebraic Approach
For those comfortable with algebra, we can solve this problem by setting up an equation. We know that 80% of a number (x) is equal to 24. We can write this as:
0.8x = 24
Dividing both sides by 0.8:
x = 24 / 0.8
x = 30
This confirms our previous findings.
Real-World Applications
Understanding percentage calculations is crucial in various real-world scenarios:
-
Finance: Calculating discounts, interest rates, taxes, profit margins, and investment returns all involve percentage calculations. For example, if a store offers an 80% discount on an item, and the discounted price is $24, you can use this method to find the original price.
-
Science: Percentage changes are used extensively in scientific research to represent variations in data, such as population growth, chemical concentrations, or experimental results.
-
Statistics: Percentages are fundamental to descriptive statistics, enabling the presentation of data in a clear and concise manner. For instance, expressing survey results as percentages allows for easy comparison and interpretation.
-
Everyday Life: Calculating tips, figuring out sale prices, and understanding nutritional information on food labels all require a grasp of percentages.
Further Exploration: Variations on the Problem
Let's consider some variations to enhance your understanding:
-
Finding the Percentage: If the problem stated "24 is what percent of 30?", you would use the formula: Percentage = (Part / Whole) * 100. In this case, (24/30) * 100 = 80%.
-
Finding the Part: If the problem were "80% of 30 is what number?", you would directly multiply 0.8 * 30 = 24.
-
Dealing with Decimals: The principles remain the same even if the numbers involve decimals. For example, "12.5 is 80% of what number?" would be solved using the same methods, resulting in x = 15.625
-
Compound Percentages: This involves calculating percentages of percentages, which is crucial for understanding compound interest. While beyond the scope of this specific problem, understanding the basic principles of percentage calculations is the first step towards mastering this complex concept.
Frequently Asked Questions (FAQ)
Q: What if the percentage is less than 100%?
A: The methods described above work regardless of whether the percentage is greater or less than 100%.
Q: Can I use a calculator for these calculations?
A: Absolutely! Calculators can significantly speed up the process, especially with more complex numbers or compound percentages.
Q: Are there other ways to solve percentage problems?
A: Yes, there are alternative methods involving ratios and proportions. However, the methods outlined here provide a solid foundation for most common percentage problems.
Q: Why is understanding percentages important?
A: Percentages are a fundamental part of mathematics with widespread applications in various aspects of life, from financial planning to scientific research and everyday decision-making. A firm grasp of percentages enables you to interpret data, make informed decisions, and solve practical problems effectively.
Conclusion
This comprehensive guide has explored multiple methods for determining what number 24 represents 80% of. We've demonstrated that 24 is 80% of 30. We've also explored the fundamental concepts of percentages, demonstrated different calculation methods, and discussed real-world applications to solidify your understanding. Mastering percentage calculations is a vital skill that empowers you to tackle a wide range of mathematical problems and confidently navigate various aspects of life involving numerical data. Remember to practice regularly and apply these techniques in different scenarios to strengthen your understanding and build confidence. With consistent effort, you'll become proficient in solving percentage problems and appreciate their importance in the world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about 24 Is 80 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.