24 Is 30 Percent Of What Number
sicesbrasil
Sep 22, 2025 · 5 min read
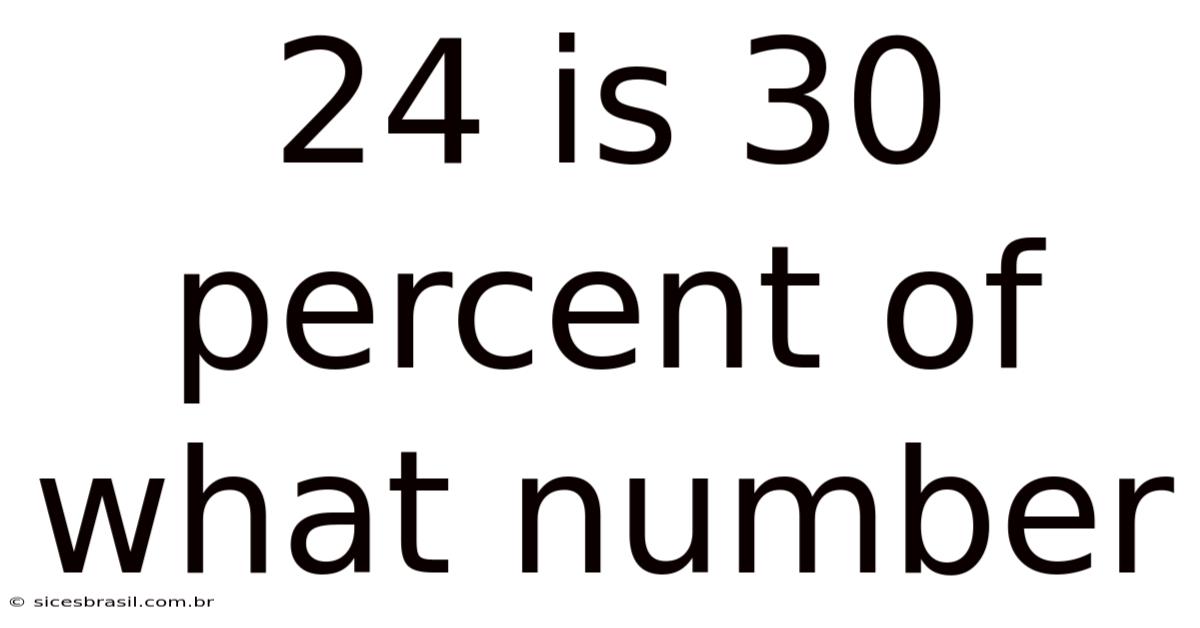
Table of Contents
24 is 30 Percent of What Number? Unlocking the World of Percentages
Finding out what number 24 represents 30% of is a fundamental problem in percentage calculations. This seemingly simple question unlocks a deeper understanding of percentages, their applications in everyday life, and the mathematical principles behind them. This article will not only provide the solution but also delve into the various methods for solving this type of problem, exploring different approaches to enhance your understanding of percentage calculations. We'll cover the basic formula, alternative methods, practical applications, and frequently asked questions to solidify your grasp on this essential mathematical concept.
Understanding Percentages: A Quick Refresher
Before we dive into solving the problem, let's briefly review the concept of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5. Understanding this fundamental principle is crucial for tackling percentage problems.
Method 1: The Formulaic Approach
The most straightforward method to solve "24 is 30 percent of what number?" involves using a basic percentage formula. The formula is:
Part = Percentage × Whole
In our problem:
- Part = 24 (this is the value we already know)
- Percentage = 30% = 0.30 (we convert the percentage to a decimal by dividing by 100)
- Whole = x (this is the unknown value we need to find)
Substituting these values into the formula, we get:
24 = 0.30 × x
To solve for x (the whole number), we need to isolate x. We can do this by dividing both sides of the equation by 0.30:
x = 24 / 0.30
x = 80
Therefore, 24 is 30 percent of 80.
Method 2: Using Proportions
Another effective way to solve this type of problem is by using proportions. We can set up a proportion as follows:
24/x = 30/100
This proportion reads: "24 is to x as 30 is to 100." We can solve this proportion using cross-multiplication:
24 × 100 = 30 × x
2400 = 30x
Now, divide both sides by 30:
x = 2400 / 30
x = 80
Again, we arrive at the solution: 24 is 30 percent of 80. This method emphasizes the relationship between the parts and the whole, offering a different perspective on the problem.
Method 3: The Reverse Percentage Calculation
This method focuses on understanding that if 24 represents 30%, then 1% would represent a smaller portion. We can find the value of 1% first, then scale up to find the 100% (the whole).
First, find the value of 1%:
24 / 30 = 0.8
This means 1% of the whole number is 0.8.
To find the whole (100%), we multiply the value of 1% by 100:
0.8 × 100 = 80
Therefore, 24 is 30 percent of 80. This method provides a clear step-by-step breakdown, making it easier to understand the underlying logic.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is essential in numerous real-world scenarios. Here are a few examples:
- Discounts and Sales: Calculating discounts on sale items is a common application of percentages. For example, if a store offers a 20% discount on a $100 item, you'd calculate the discount as 20% of $100, which is $20, and the final price would be $80.
- Taxes and Interest: Calculating sales tax, income tax, or interest on loans or investments involves percentages. For example, if the sales tax is 6%, you would calculate the tax amount on the purchase price and add it to find the total cost.
- Tips and Gratuities: Calculating tips in restaurants or service charges often involves percentages. A common tip is 15% or 20% of the bill.
- Statistics and Data Analysis: Percentages are frequently used in representing data and analyzing trends in various fields, such as economics, demographics, and scientific research.
- Financial Planning: Budgeting, savings, and investment strategies often require understanding and calculating percentages. For example, determining the percentage of income allocated to different expenses.
Beyond the Basics: More Complex Percentage Problems
While the problem "24 is 30 percent of what number?" is relatively simple, the principles involved can be applied to more complex scenarios. For instance:
- Finding the percentage increase or decrease: Calculating the percentage change between two values requires understanding how to express the difference as a percentage of the original value.
- Compound interest calculations: Compound interest involves applying interest to the principal amount plus accumulated interest, leading to exponential growth.
- Percentage calculations with multiple percentages: Some problems involve multiple percentage changes, requiring a sequential calculation or a more advanced understanding of percentage manipulation.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve percentage problems?
A: Absolutely! Calculators are a valuable tool for solving percentage problems, especially more complex ones. Most calculators have a percentage function (%) that simplifies the calculations.
Q: What if the percentage is greater than 100%?
A: If the percentage is greater than 100%, it means the "part" is larger than the "whole." This often occurs when dealing with percentage increases or growth rates. The formula remains the same, but the result will be a number larger than the "part."
Q: Are there any other methods to solve percentage problems?
A: Yes, there are alternative methods, such as using ratios, proportions, or even graphical representations depending on the complexity of the problem and your personal preference. The choice of method often depends on the specific problem and your level of comfort with different mathematical techniques.
Q: Why is understanding percentages important?
A: Understanding percentages is a crucial life skill. It allows you to interpret data, make informed decisions in financial matters, and comprehend information presented in various contexts, from news reports to scientific studies.
Conclusion: Mastering Percentage Calculations
Solving the problem "24 is 30 percent of what number?" is not just about finding the answer (80). It’s about understanding the underlying principles of percentage calculations and their wide-ranging applications. By mastering these fundamental concepts, you equip yourself with a valuable skill applicable across numerous aspects of daily life, from personal finance to professional endeavors. Whether you use the formulaic approach, the proportion method, or the reverse percentage calculation, the key is to grasp the underlying logic and choose the method most comfortable for you. The more you practice, the more confident and proficient you will become in solving percentage problems of any complexity. Remember, understanding percentages is a building block for more advanced mathematical concepts, and mastering it will pave the way for success in various fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about 24 Is 30 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.