20 As A Percentage Of 50
sicesbrasil
Sep 24, 2025 · 5 min read
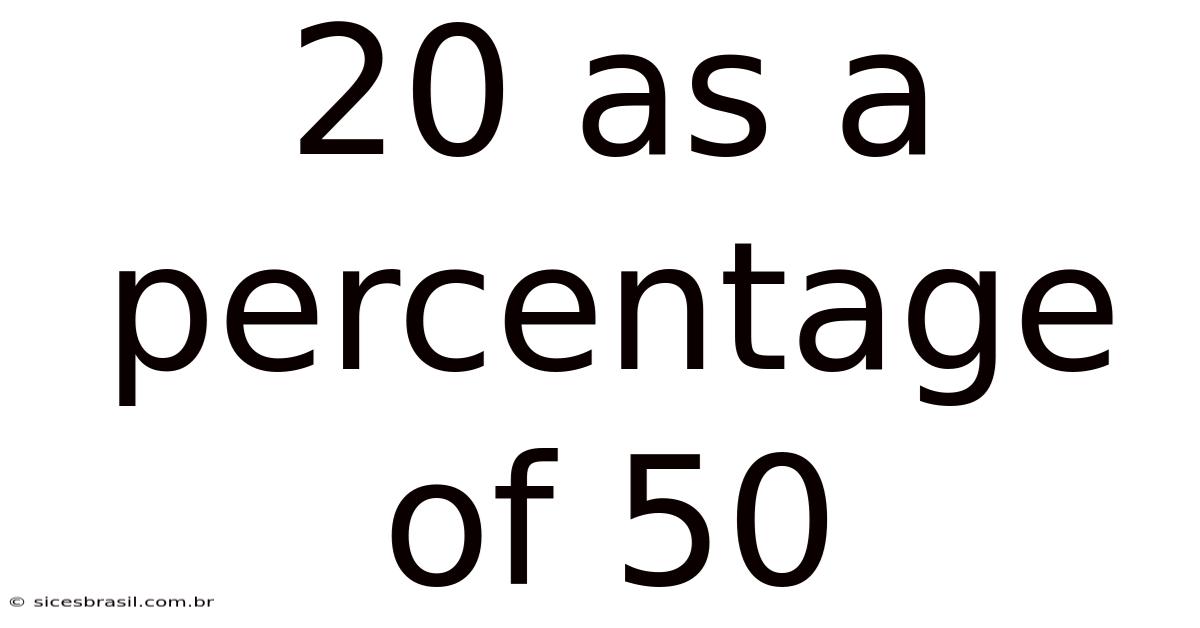
Table of Contents
20 as a Percentage of 50: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This article delves deep into calculating "20 as a percentage of 50," providing a step-by-step guide, explaining the underlying mathematical principles, and exploring relevant applications. We will also tackle common misconceptions and offer practical examples to solidify your understanding. This guide aims to equip you with not just the answer, but a comprehensive understanding of percentage calculations.
Introduction: Understanding Percentages
A percentage is a fraction or a ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Therefore, calculating a percentage involves determining what proportion of a whole a particular part represents, expressed as a fraction of 100. This is crucial in various fields, including finance, statistics, science, and everyday life.
Calculating 20 as a Percentage of 50: A Step-by-Step Approach
To calculate 20 as a percentage of 50, we follow these simple steps:
-
Formulate the Fraction: First, express the given numbers as a fraction. In this case, 20 is the part, and 50 is the whole. Therefore, the fraction is 20/50.
-
Convert the Fraction to a Decimal: Divide the numerator (20) by the denominator (50). This gives us 0.4.
-
Convert the Decimal to a Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the percent sign (%). Thus, 0.4 * 100 = 40%.
Therefore, 20 is 40% of 50.
The Mathematical Formula: A Deeper Dive
The calculation above can be generalized into a formula:
(Part / Whole) * 100% = Percentage
Where:
- Part: The value you want to express as a percentage of the whole.
- Whole: The total value.
- Percentage: The resulting percentage.
Using this formula for our example:
(20 / 50) * 100% = 40%
Real-World Applications and Examples
Understanding percentages is vital in numerous real-world scenarios. Here are a few examples demonstrating the practical application of this concept:
-
Sales and Discounts: A store offers a 40% discount on an item originally priced at $50. Using our knowledge, we know that the discount is $20 ($50 * 0.40 = $20). The final price after the discount would be $30.
-
Tax Calculations: If the sales tax rate is 8%, and you purchase an item for $50, the tax amount would be $4 ($50 * 0.08 = $4).
-
Grade Calculations: If you scored 20 points out of a possible 50 points on a test, your score would be 40%.
-
Data Analysis: In data analysis, percentages are frequently used to represent proportions within datasets, making comparisons and interpretations easier. For example, if 20 out of 50 surveyed people prefer a certain product, then 40% of the surveyed people prefer that product.
Common Misconceptions and Pitfalls
While percentage calculations are straightforward, some common misconceptions can lead to errors. Let's address a few:
-
Confusing Part and Whole: Always carefully identify the part and the whole. Incorrectly identifying these can lead to incorrect results.
-
Incorrect Decimal-to-Percentage Conversion: Remember to multiply by 100 when converting a decimal to a percentage. Forgetting this step is a frequent mistake.
-
Overcomplicating Simple Calculations: While understanding the underlying formula is crucial, many percentage calculations can be solved mentally or using simple arithmetic. Don't overcomplicate the process.
Expanding the Concept: Percentage Increase and Decrease
The concept of percentage extends beyond simply finding a percentage of a whole. We often encounter situations involving percentage increases or decreases.
-
Percentage Increase: Suppose a value increases from 50 to 70. The increase is 20 (70 - 50 = 20). The percentage increase is calculated as: (Increase/Original Value) * 100% = (20/50) * 100% = 40%. Therefore, there is a 40% increase.
-
Percentage Decrease: Suppose a value decreases from 50 to 30. The decrease is 20 (50 - 30 = 20). The percentage decrease is calculated as: (Decrease/Original Value) * 100% = (20/50) * 100% = 40%. Therefore, there is a 40% decrease.
Advanced Applications: Compound Interest and Growth Rates
Percentages play a crucial role in more complex financial calculations like compound interest and growth rates.
-
Compound Interest: Compound interest is calculated on the principal amount plus any accumulated interest. Understanding percentage calculations is essential to calculate the total amount after a certain period with compound interest.
-
Growth Rates: In economics and finance, growth rates (like GDP growth or investment returns) are expressed as percentages to represent the rate of change over time.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage of a number mentally?
A1: For simple calculations, you can use mental math. For example, to find 10% of a number, simply divide by 10. To find 50%, divide by 2. You can then combine these to find other percentages. For example, 15% of 50 is 10% (5) + 5% (2.5) = 7.5.
Q2: What if the "whole" is zero?
A2: You cannot calculate a percentage when the whole is zero. Division by zero is undefined in mathematics.
Q3: Can I use a calculator for percentage calculations?
A3: Absolutely! Calculators are a helpful tool for percentage calculations, especially for more complex problems. Many calculators have a dedicated percentage function.
Q4: Are there different ways to express percentages?
A4: Yes, percentages can also be expressed as decimals (0.40) or fractions (2/5).
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, such as determining 20 as a percentage of 50 (which is 40%), is a valuable skill with widespread applications. This article provides a comprehensive guide, covering the fundamental concepts, step-by-step calculations, real-world examples, and common pitfalls. By mastering these principles, you'll be well-equipped to tackle percentage problems confidently and efficiently in various contexts, enhancing your problem-solving abilities and understanding of numerical data. Remember that consistent practice is key to solidifying your understanding and improving your speed and accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about 20 As A Percentage Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.