1 And 1 8 As A Decimal
sicesbrasil
Sep 22, 2025 · 5 min read
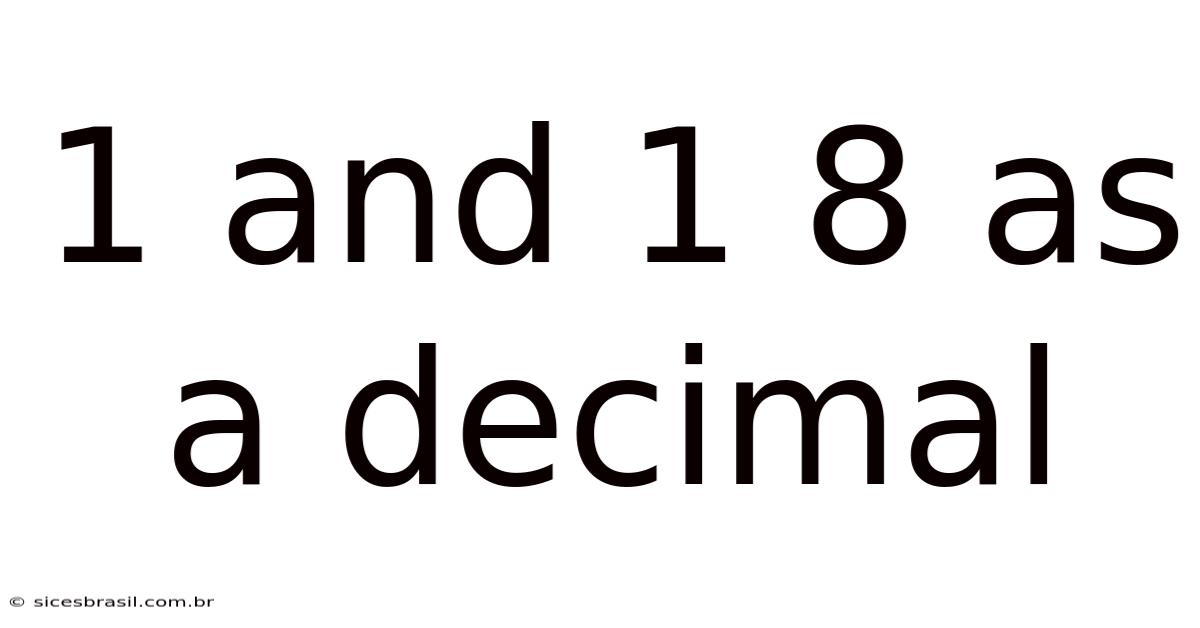
Table of Contents
Understanding 1 and 1/8 as a Decimal: A Comprehensive Guide
The seemingly simple question of converting the mixed number 1 and 1/8 into its decimal equivalent opens a door to a deeper understanding of fractions, decimals, and the fundamental relationship between these two crucial mathematical representations. This comprehensive guide will explore this conversion, explaining the process in detail, delving into the underlying mathematical principles, and providing practical examples to solidify your understanding. We'll also address common questions and misconceptions surrounding decimal representation.
Understanding Fractions and Decimals
Before diving into the specific conversion of 1 and 1/8, let's establish a solid foundation. Fractions represent parts of a whole. The numerator (top number) indicates the number of parts we have, while the denominator (bottom number) indicates the total number of equal parts the whole is divided into. Decimals, on the other hand, represent numbers based on powers of 10. They use a decimal point to separate the whole number part from the fractional part. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on.
For example, 0.5 represents five-tenths (5/10), 0.25 represents twenty-five hundredths (25/100), and so on. The core concept linking fractions and decimals is the idea of representing a portion of a whole using different notations. The ability to convert between these representations is crucial for many mathematical operations and real-world applications.
Converting 1 and 1/8 to a Decimal: Step-by-Step
The mixed number 1 and 1/8 signifies one whole unit plus one-eighth of another unit. To convert this to a decimal, we need to transform the fractional part (1/8) into its decimal equivalent. Here's the step-by-step process:
Step 1: Divide the Numerator by the Denominator
The simplest approach is to perform the division: 1 ÷ 8. This will give us the decimal representation of the fraction 1/8.
1 ÷ 8 = 0.125
Step 2: Add the Whole Number
Now that we have the decimal equivalent of 1/8 (0.125), we simply add it to the whole number part of the mixed number, which is 1.
1 + 0.125 = 1.125
Therefore, 1 and 1/8 as a decimal is 1.125.
Alternative Methods for Conversion
While the direct division method is straightforward, let's explore other methods to deepen your understanding and enhance your problem-solving skills.
Method 2: Converting to an Improper Fraction
A mixed number can be converted into an improper fraction (where the numerator is greater than or equal to the denominator). To do this:
- Multiply the whole number by the denominator: 1 * 8 = 8
- Add the numerator: 8 + 1 = 9
- Keep the same denominator: 9/8
Now, divide the numerator (9) by the denominator (8):
9 ÷ 8 = 1.125
This confirms our previous result.
Method 3: Using Equivalent Fractions
We can find an equivalent fraction with a denominator that is a power of 10. However, in this case, it's not easily achievable. While we could find a common denominator with a power of 10 (like 1000), the calculations would be more complex than the direct division method. This method is more efficient when dealing with fractions that have denominators which are easily converted to powers of 10 (e.g., fractions with denominators of 2, 4, 5, 10, 20, 25, 50, and 100).
Understanding the Decimal Place Value
The decimal 1.125 can be broken down as follows:
- 1: Represents one whole unit.
- 0.1: Represents one-tenth (1/10).
- 0.02: Represents two-hundredths (2/100).
- 0.005: Represents five-thousandths (5/1000).
This highlights the relationship between the decimal representation and the fractional representation. Each digit to the right of the decimal point represents a progressively smaller fraction of a whole.
Practical Applications
The ability to convert between fractions and decimals is fundamental in many areas, including:
- Measurement: Many measurement systems use both fractions (e.g., inches) and decimals (e.g., centimeters). Converting between them allows for accurate calculations and comparisons.
- Finance: Calculating interest rates, discounts, and other financial calculations often involve converting fractions to decimals.
- Engineering: Precision engineering relies heavily on accurate decimal representations for dimensions and calculations.
- Computer Science: Binary numbers (base-2) are fundamental in computing, and converting between binary, decimal, and fractional representations is crucial for programmers.
- Everyday Life: Dividing recipes, calculating distances, or even understanding sales percentages all utilize the principles of fraction-to-decimal conversion.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to terminating decimals?
A: No. Fractions with denominators that have prime factors other than 2 and 5 will result in repeating decimals (e.g., 1/3 = 0.333...). 1/8, however, has a denominator (8 = 2³) which only contains the prime factor 2, resulting in a terminating decimal.
Q: What if I have a larger mixed number?
A: The process remains the same. Convert the fractional part to a decimal by division and then add the whole number part. For example, 3 and 3/4: 3/4 = 0.75, so 3 and 3/4 = 3.75.
Q: Are there any online tools to help with this conversion?
A: Yes, many online calculators and converters can perform fraction-to-decimal conversions. These tools can be useful for checking your work or for handling more complex conversions. However, understanding the underlying principles is essential for true mathematical proficiency.
Q: Why is it important to learn this conversion?
A: This conversion skill builds a crucial foundation in understanding numerical representation. It improves your ability to perform calculations, solve problems, and interpret data across various fields. It strengthens your overall mathematical understanding and problem-solving abilities.
Conclusion
Converting 1 and 1/8 to a decimal (1.125) is a fundamental exercise that showcases the interrelationship between fractions and decimals. Understanding the methods outlined—direct division, converting to an improper fraction, and exploring equivalent fractions—provides a comprehensive grasp of the concept. This knowledge extends far beyond simple conversions, paving the way for a more profound understanding of numbers and their practical applications in various fields. Remember, mastering this seemingly basic conversion builds a strong foundation for more advanced mathematical concepts. Practice makes perfect, so try converting different fractions and mixed numbers to decimals to solidify your understanding and build confidence in your mathematical skills. The ability to seamlessly move between fractional and decimal representations is a valuable asset in various aspects of life and learning.
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 And 1 8 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.