1 1/8 As A Decimal

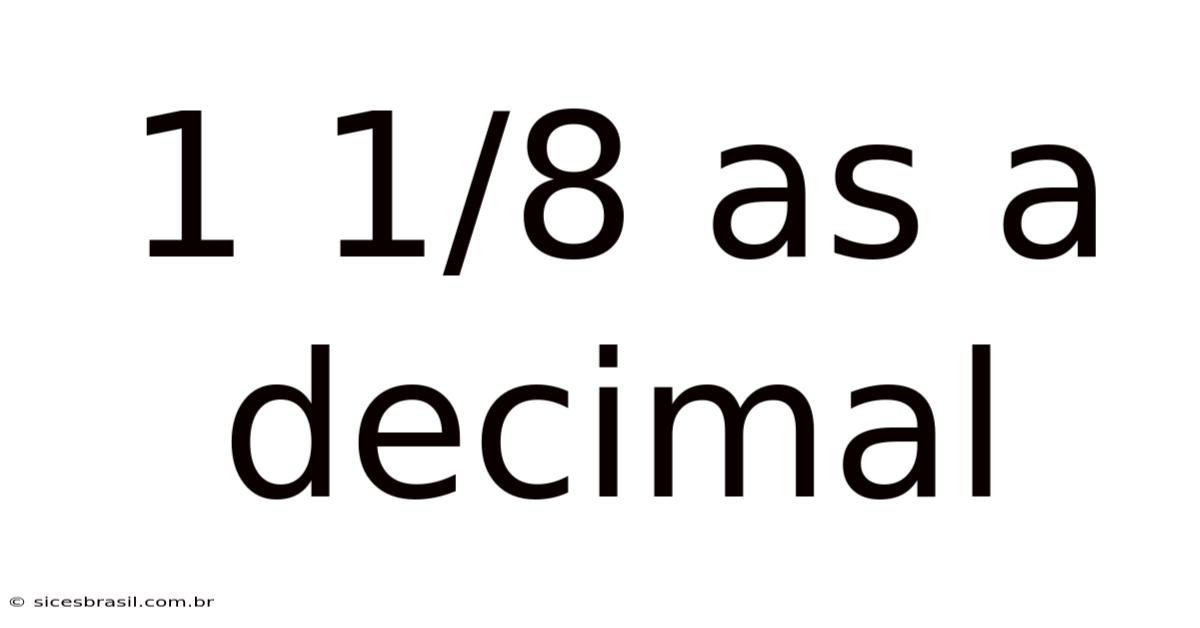
1 1/8 as a Decimal: A full breakdown

Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. Now, this thorough look will look at converting the mixed number 1 1/8 into its decimal form, exploring the underlying concepts and providing practical applications. In practice, we'll cover various methods, address common misconceptions, and equip you with the knowledge to confidently tackle similar conversions. This guide is perfect for students, educators, and anyone seeking a deeper understanding of fractions and decimals Not complicated — just consistent..

Understanding Mixed Numbers and Decimals

Before we dive into the conversion process, let's refresh our understanding of key terms. A mixed number combines a whole number and a fraction, like 1 1/8. A decimal, on the other hand, represents a number using a base-ten system, with a decimal point separating the whole number part from the fractional part (e.g., 1.But 125). Converting between these forms involves understanding the relationship between fractions and their decimal representations Nothing fancy..

Method 1: Converting the Fraction to a Decimal, Then Adding the Whole Number

This is perhaps the most straightforward method. We'll first convert the fraction 1/8 into a decimal and then add the whole number 1 Most people skip this — try not to. That's the whole idea..

Divide the numerator by the denominator: To convert 1/8 to a decimal, we divide the numerator (1) by the denominator (8): 1 ÷ 8 = 0.125
Add the whole number: Now, we add the whole number part (1) to the decimal equivalent of the fraction: 1 + 0.125 = 1.125

Which means, 1 1/8 as a decimal is 1.125.

Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal

This method involves converting the mixed number into an improper fraction first, and then converting that improper fraction into a decimal.

Convert to an improper fraction: To convert 1 1/8 to an improper fraction, we multiply the whole number (1) by the denominator (8), add the numerator (1), and keep the same denominator: (1 * 8) + 1 = 9, so the improper fraction is 9/8.
Divide the numerator by the denominator: Now, we divide the numerator (9) by the denominator (8): 9 ÷ 8 = 1.125

Again, we arrive at the same result: 1 1/8 as a decimal is 1.125.

Method 3: Using Decimal Equivalents of Common Fractions

Knowing the decimal equivalents of common fractions can significantly speed up the conversion process. But for example, knowing that 1/8 = 0. Memorizing the decimal equivalents of fractions like 1/2 (0.Also, 125. 125 allows for immediate conversion: 1 + 0.Because of that, 125), 1/10 (0. Because of that, 1), etc. Worth adding: 5), 1/4 (0. Plus, 25), 1/8 (0. In practice, 125 = 1. , is a valuable skill for quick mental calculations It's one of those things that adds up..

Understanding the Decimal Place Value

The decimal 1.125 can be broken down into its place values:

1: Represents one whole unit.
1: Represents one-tenth (1/10).
2: Represents two-hundredths (2/100).
5: Represents five-thousandths (5/1000).

Understanding place value is crucial for comprehending the magnitude of each digit in a decimal number The details matter here..

Practical Applications of Decimal Conversion

Converting fractions to decimals is essential in numerous real-world applications:

Measurements: Many measurement systems, particularly in science and engineering, use decimal notation. Converting fractions to decimals is necessary for accurate calculations and comparisons. As an example, if a recipe calls for 1 1/8 cups of flour, knowing the decimal equivalent (1.125 cups) might be helpful when using measuring cups with decimal markings Easy to understand, harder to ignore..
Finance: In financial calculations, decimals are commonly used to represent monetary values. Understanding decimal equivalents of fractions is crucial for calculating interest, discounts, and other financial aspects.
Data Analysis: In data analysis and statistics, converting fractions to decimals facilitates calculations and comparisons between different data points. This is especially important when dealing with percentages and proportions The details matter here..
Computer Programming: Computers work with binary numbers, but often represent and display data using decimal notation. Understanding fraction-to-decimal conversions is fundamental in computer programming and data manipulation.

Common Misconceptions and Pitfalls

Incorrectly placing the decimal point: A common mistake is placing the decimal point incorrectly during the division process. Carefully align the digits and ensure the decimal point is correctly positioned in the quotient.
Confusing numerator and denominator: Remember to always divide the numerator by the denominator. Dividing the denominator by the numerator will lead to an incorrect result That's the whole idea..
Rounding errors: When working with decimals, rounding can introduce errors, especially when performing multiple calculations. it helps to use sufficient decimal places to minimize the impact of rounding errors Not complicated — just consistent..

Frequently Asked Questions (FAQ)

Q: Can I convert any fraction to a decimal?

A: Yes, any fraction can be converted to a decimal by dividing the numerator by the denominator. The resulting decimal might be terminating (like 1.125) or repeating (like 1/3 = 0.333...).

Q: What if the fraction is a larger mixed number, like 5 3/16?

A: The same principles apply. You can either convert the fraction 3/16 to a decimal first (3 ÷ 16 = 0.1875) and then add the whole number (5 + 0.1875 = 5.1875) or convert the mixed number to an improper fraction (83/16) and then divide.

Q: Are there any online tools to help with fraction-to-decimal conversion?

A: Yes, many online calculators and converters are available to assist with fraction-to-decimal conversions. These tools can be useful for verifying your calculations and exploring different conversion methods.

Q: How do I convert a repeating decimal back to a fraction?

A: Converting a repeating decimal back to a fraction involves a slightly more complex process, often using algebraic manipulation. The method typically involves setting the repeating decimal equal to a variable, multiplying by a power of 10 to shift the decimal point, and then subtracting the original equation to eliminate the repeating part. This process results in an equation that can be solved for the variable, which represents the fractional equivalent.

Conclusion

Converting 1 1/8 to its decimal equivalent (1.125) is a straightforward process that involves understanding the relationship between fractions and decimals. Mastering this conversion is crucial for success in various mathematical applications and real-world scenarios. That said, we've explored multiple methods, highlighting the importance of place value and addressing common misconceptions. Remember to practice regularly and familiarize yourself with the decimal equivalents of common fractions to enhance your mathematical proficiency. The ability to without friction move between fractions and decimals significantly improves your problem-solving skills and allows for a deeper understanding of numerical representation Easy to understand, harder to ignore..